Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác \(MNP\) tam giác \(DEF\) ta có:
\(\widehat M = \widehat D\) (giả thuyết)
\(\widehat N = \widehat E\) (giả thuyết)
Do đó, \(\Delta MNP\backsim\Delta DEF\) (g.g)
Suy ra, \(\frac{{MP}}{{DF}} = \frac{{NP}}{{EF}} \Rightarrow \frac{{18}}{{24}} = \frac{{a + 2}}{{32}} \Rightarrow a + 2 = \frac{{18.32}}{{24}} = 24 \Leftrightarrow a = 24 - 2 = 22\).
Vậy \(a = 22m\).
b) Vì \(ABCD\) là hình thang nên \(AB//CD\).
Vì \(AB//CD \Rightarrow \widehat {ABM} = \widehat {MDC}\) (hai góc so le trong) và \(AB//CD \Rightarrow \widehat {BAM} = \widehat {MCD}\) (hai góc so le trong)
Xét tam giác \(AMB\) và tam giác \(CMD\) có:
\(\widehat {ABM} = \widehat {MDC}\) (chứng minh trên)
\(\widehat {BAM} = \widehat {MCD}\) (chứng minh trên)
Do đó, \(\Delta AMB\backsim\Delta CMD\) (g.g).
Ta có:
\(\frac{{AM}}{{CM}} = \frac{{BM}}{{DM}} = \frac{{AB}}{{CD}} \Leftrightarrow \frac{6}{{15}} = \frac{y}{{10}} = \frac{8}{x}\).
Ta có: \(\frac{6}{{15}} = \frac{y}{{10}} \Rightarrow y = \frac{{10.6}}{{15}} = 4\)
\(\frac{6}{{15}} = \frac{8}{x} \Rightarrow x = \frac{{8.15}}{6} = 20\).
Vậy \(x = 20;y = 4\).

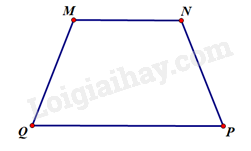
a) Hình thang \(MNPQ\) có \(\widehat Q = 90^\circ \) nên là hình thang vuông. Suy ra \(\widehat M = 90^\circ \)
Áp dụng định lí tổng các góc của một tứ giác, ta có: \(\widehat P = 360^\circ - \left( {90^\circ + 90^\circ + 125^\circ } \right) = 55^\circ \)
b) Hình thang \(MNPQ\) có \(\widehat P = \widehat Q = 110^\circ \) nên là hình thang cân.
Suy ra \(\widehat M = \widehat N = 180^\circ - 110^\circ = 70^\circ \)

Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\ \Rightarrow 70^\circ + 80^\circ + \widehat C = 180^\circ \\ \Rightarrow \widehat C = 30^\circ \end{array}\)
Xét tam giác ABC và tam giác PMN có:
\(\begin{array}{l}\widehat B = \widehat M = 80^\circ \\\widehat C = \widehat N = 30^\circ \end{array}\)
\( \Rightarrow \Delta ABC \backsim \Delta PMN\) (g-g)
\( \Rightarrow \frac{{AB}}{{PM}} = \frac{{BC}}{{MN}} = \frac{{CA}}{{NP}}\) (Tỉ số đồng dạng)

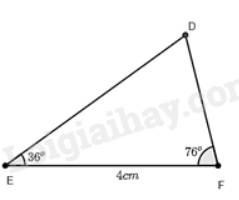
a) Xét tam giác \(DEF\) và tam giác \(AMC\) có:
\(\widehat E = \widehat M = 36^\circ \)
\(\widehat F = \widehat C = 76^\circ \) (chứng minh trên)
Suy ra, \(\Delta DEF\backsim\Delta AMC\) (g.g).
b) Đổi 25m = 2500 cm.
Dùng thước đo độ dài cạnh \(DF\) ta được độ dài \(DF\) là 2,6cm.
Vì \(\Delta DEF\backsim\Delta AMC\) nên \(\frac{{DF}}{{EF}} = \frac{{AC}}{{MC}}\) (hai cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{2,6}}{4} = \frac{{AC}}{{2500}} \Rightarrow AC = \frac{{2,6.2500}}{4} = 1625\).
Vậy khoảng cách giữa hai điểm \(A\) và \(C\) là 1625 cm hay 16,25m.

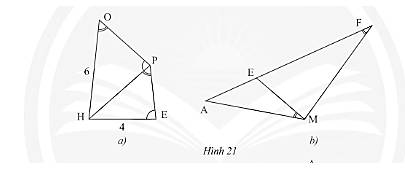
a) Xét tam giác \(OPH\) tam giác \(PEH\) ta có:
\(\widehat {HOP} = \widehat {HPE}\) (giả thuyết)
\(\widehat {OPH} = \widehat {PEH}\) (giả thuyết)
Do đó, \(\Delta OPH\backsim\Delta PEH\) (g.g)
Suy ra, \(\frac{{PH}}{{EH}} = \frac{{OH}}{{PH}} \Rightarrow P{H^2} = OH.EH = 4.6 \Rightarrow P{H^2} = 24 \Leftrightarrow PH = \sqrt {24} = 2\sqrt 6 \).
Vậy \(PH = 2\sqrt 6 \).
b) Xét tam giác \(AME\) tam giác \(AFM\) ta có:
\(\widehat {AME} = \widehat {AFM}\) (giả thuyết)
\(\widehat A\) chung
Do đó, \(\Delta AME\backsim\Delta AFM\) (g.g)
Suy ra, \(\frac{{AM}}{{AF}} = \frac{{AE}}{{AM}} \Rightarrow A{M^2} = AF.AE\) (điều phải chứng minh).

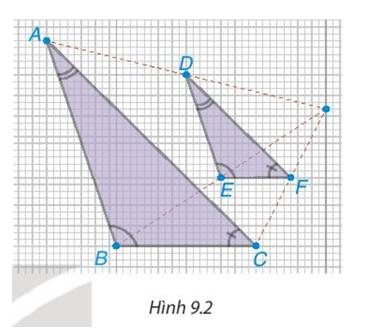
Ta có: \(\frac{{AB}}{{DE}} = 2{;^{}}\frac{{BC}}{{EF}} = 2{;^{}}\frac{{AC}}{{DF}} = 2\)
Ta có:\(\dfrac{AB}{DE}=2;\dfrac{BC}{EF}=2;\dfrac{AC}{DF}=2\)
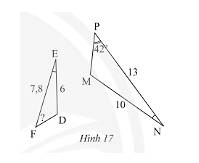



Ta có:
\(\frac{{EF}}{{NP}} = \frac{{7,8}}{{13}} = \frac{3}{5};\frac{{DE}}{{MN}} = \frac{6}{{10}} = \frac{3}{5}\)
Xét tam giác \(DEF\) và tam giác \(MNP\) ta có:
\(\frac{{EF}}{{NP}} = \frac{{DE}}{{MN}} = \frac{3}{5}\)
\(\widehat E = \widehat N\) (giải thuyết)
Do đó, \(\Delta DEF\backsim\Delta MNP\) (c.g.c)
Do đó, \(\widehat F = \widehat P = 42^\circ \).