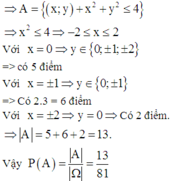Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn B
Ta có ![]()
Do đó ![]()
Ta cũng có ![]() => n(A) = 8
=> n(A) = 8
Vậy xác suất của biến cố A là P(A) = 8 21

Đáp án A
Để con châu chấu đáp xuống các điểm M(x; y) có x + y < 2 thì con châu chấu sẽ nhảy trong khu vực hình thang BEIA
Để M(x; y) có tọa độ nguyên thì x ∈ - 2 ; - 1 ; 0 ; 1 ; 2 , y ∈ { 0 ; 1 ; 2 }
Nếu x ∈ - 2 ; - 1 thì y ∈ { 0 ; 1 ; 2 } có 2.3 = 6 điểm
Nếu x = 0 thì y ∈ { 0 ; 1 } có 2 điểm
Nếu x =1 => y = 0 => có 1 điểm
=> có tất cả 6 + 2 + 1 = 9 điểm. Để con châu chấu nhảy trong hình chữ nhật mà đáp xuống các điểm có tọa độ nguyên thì x ∈ - 2 ; - 1 ; 0 ; 1 ; 2 ; 3 ; 4 , y ∈ { 0 ; 1 ; 2 } . Số các điểm M(x; y) có tọa độ nguyên là: 7.3 = 21 điểm. Xác suất cần tìm là: P = 9 21 = 3 7 .

Chọn C
Lời giải. Số các điểm có tọa độ nguyên thuộc hình chữ nhật là 7.3 = 21 điểm vì
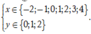
Để con châu chấu đáp xuống các điểm M(x,y) có x + y < 2
thì con châu chấu sẽ nhảy trong khu vực hình thang BEIA
Để M(x,y) có tọa độ nguyên thì
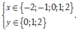
= Nếu x ∈ - 2 ; - 1 thì y ∈ 0 ; 1 ; 2
⇒ có 6 điểm
= Nếu x = 0 thì y ∈ 0 ; 1 ⇒ có 2 điểm
= Nếu x = 1 ⇒ y = 0 ⇒ có 1 điểm
⇒ có tất cả 6 + 2 +1 = 9 điểm thỏa mãn
Vậy xác suất cần tính P = 9 21 = 3 7

Đáp án D
Số phần tử của không gian mẫu tập hợp các điểm có tọa độ nguyên nằm trên hình chữ nhật OMNP là
n Ω = 101 x 11
![]()
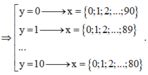
Khi đó có 91 + 90 + . . . + 81 = 946 cặp (x;y) thỏa mãn
Vậy xác suất cần tính là
![]()

Điểm A(x;y) nằm bên trong (kể cả trên cạnh) của
![]()
Có 101 cách chọn x, 11 cách chọn y. Do đó số phần tử của không gian mẫu tập hợp các điểm có tọa độ nguyên nằm trên hình chữ nhật OMNP là n( Ω ) = 101 x 11
Gọi X là biến cố: “Các điểm A(x;y) thỏa mãn x + y ≤ 90”.
Vì
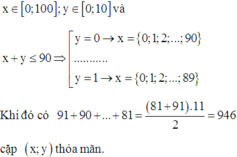
Vậy xác suất cần tính là
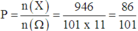

Đáp án A
Phương pháp:
+) Biểu diễn không gian mẫu dưới dạng tập hợp
![]()
tìm Ω
+) Gọi A là biến cố: “Tập hợp các điểm mà khoảng cách đến gốc tọa độ nhỏ hơn hoặc bằng 2”, biểu diễn A dưới dạng tập hợp và tìm số phần tử của A.
+) Tính xác suất của biến cố A: P(A) = A Ω
Cách giải:
Không gian mẫu
![]()
Có 9 cách chọn x, 9 cách chọn y, do đó Ω = 9.9 = 81
Tập hợp các điểm mà khoảng cách đến gốc tọa độ nhỏ hơn hoặc bằng 2 là hình tròn tâm O bán kính 2.
Gọi A là biến cố: “ Tập hợp các điểm mà khoảng cách đến gốc tọa độ nhỏ hơn hoặc bằng 2”