Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
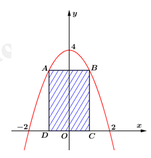 Gọi S là diện tích hình phẳng giới hạn bởi Parabol có phương trình
y
=
4
-
x
2
và trục hoành
Gọi S là diện tích hình phẳng giới hạn bởi Parabol có phương trình
y
=
4
-
x
2
và trục hoành
Suy ra ∫ - 2 2 4 - x 2 d x = 32 3 m 2
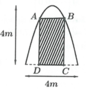
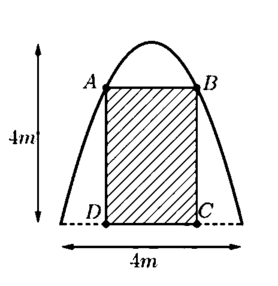
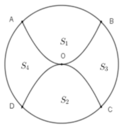
Gọi điểm C a ; 0 , a > 0 ⇒ D - a ; 0 B ( a ; 4 - a 2 ) , A - a ; 4 - a 2
Gọi S 1 là diện tích ABCD, suy ra S 1 = A B . B C = 2 a . 4 - a 2 m 2
Gọi S 2 là diện tích có hoa văn, suy ra S 2 = S - S 1
S 2 nhỏ nhất khi và chỉ khi S 1 lớn nhất
Xét hàm số f a = 2 a 4 - a 2 , a ∈ 0 ; 4
Ta có f ' a = 8 - 6 a 2 ⇒ f ' a = 0 ⇔ a = 2 3
Xét bảng biến thiên hàm số f(a) với a ∈ 0 ; 4
Suy ra m a x 0 ; 4 f a = f 2 3 = 32 3 9 m 2 . Suy ra S 2 m i n = 32 3 - 32 3 9 ≈ 4 , 51 m 2
Suy ra số tiền cần bằng 902.000 đồng.

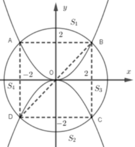
Chọn đáp án B
Phương pháp
+ Từ giả thiết ta viết được phương trình đường tròn và phương trình parabol
+ S 1 là phần diện tích giới hạn bởi parabol; đường tròn và hai đường thẳng x=2;x=-2. Từ đó sử dụng công thức diện tích hình phẳng bằng ứng dụng tích phân để tính S 1 .
Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y=f(x);y=g(x) và hai đường thẳng x=a;x=b là
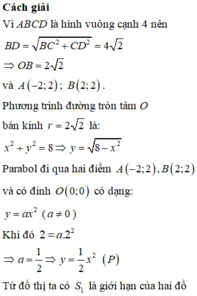
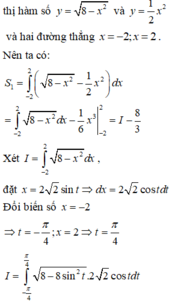
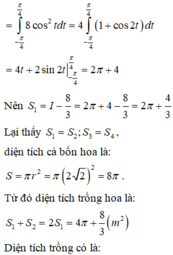
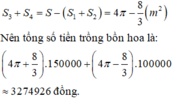

Đáp án B.
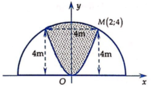 Đặt hệ trục tọa độ như hình vẽ. Khi đó phương trình nửa đường tròn là
y
=
R
2
-
x
2
=
2
5
2
-
x
2
=
20
-
x
2
.
Đặt hệ trục tọa độ như hình vẽ. Khi đó phương trình nửa đường tròn là
y
=
R
2
-
x
2
=
2
5
2
-
x
2
=
20
-
x
2
.
Phương trình parabol (P) có đỉnh là gốc O sẽ có dạng y = a x 2 . Mặt khác (P) qua điểm M(2;4) do đó 4 = a . - 2 2 ⇔ a = 1 .
Phần diện tích của hình phẳng giới hạn bởi (P) và nửa đường tròn (phần tô màu) là S 1 = ∫ - 2 2 20 - x 2 - x 2 d x ≈ 11 , 94 ( m 2 ) .
Phần diện tích trồng cỏ là: S t r o n g c o = 1 2 S h i n h t r o n - S 1 ≈ 19 , 47592654 m 2 .
Vậy số tiền cần có là S t r o n g c o × 100000 ≈ 1948000 (đồng).

Chọn C.
Phương pháp: Sử dụng tích phân để tính.
Cách giải: Vì hình có tính chất đối xứng nên ta tính phần diện tích ở góc
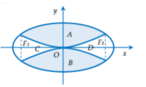
Phương trình đường elip ở nửa trên là ![]()



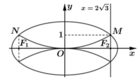
Diện tích Elip: ![]()
Chọn hệ trục tọa độ và gọi các điểm như hình.
Phương trình Elip là: ![]()
Suy ra đường Elip nằm trên trục Ox là: ![]()
Giao điểm của đường thẳng d:
x
=
2
3
đi qua tiêu điểm
F
2
và nửa Elip nằm bên trên trục Ox là ![]()
Parabol đi qua các điểm ![]() có phương trình
có phương trình ![]()
Khi đó diện tích 
Khi đó diện tích
Vậy số tiền cần chi phí: ![]()
Chọn D.

Phương pháp:
+ Tìm phương trình Parabol
+ Diện tích hình phẳng giới hạn bởi
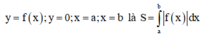
+ Tính diện tích hình chữ nhật từ đó tính diện tích phần trồng hoa và tính số tiền cần dùng để mua hoa trang trí.
Cách giải:
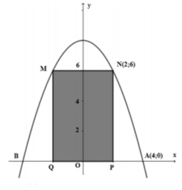
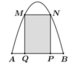
Gắn hệ trục tọa độ Oxy như hình vẽ, ta có Parabol đi qua các điểm A 4 ; 0 ; N 2 ; 6

Hoành độ giao điểm của Parabol và trục hoành là


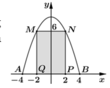
Chọn hệ trục tọa độ Oxy như hình vẽ.
Parabol đối xứng qua Oy nên có dạng ![]()
Vì (P) đi qua B(4;0) và N(2;6) nên ![]()
Diện tích hình phẳng giới hạn bởi (P) và trục Ox là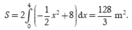
Diện tích phần trồng hoa là ![]()
Do đó số tiền cần dùng để mua hoa là ![]()
Chọn D.
 Chi phí dán hoa văn là 200.000 đồng cho một
m
2
bảng. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên pano sẽ là bao nhiêu (làm tròn đến hàng nghìn)?
Chi phí dán hoa văn là 200.000 đồng cho một
m
2
bảng. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên pano sẽ là bao nhiêu (làm tròn đến hàng nghìn)?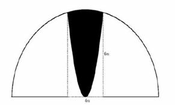







Chọn hệ trục tọa độ như hình vẽ. Khi đó phương trình Parabol có dạng:
Gọi là diện tích hình phẳng giới hạn bởi Parabol có phương trình y = 4 - x 2 và trục hoành.