Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích tam giác ABC: \(S = \frac{1}{2}ac.\sin B\)
Mà \(\widehat B = {135^o} \Rightarrow \sin B = \sin {135^o} = \frac{{\sqrt 2 }}{2}\).
\( \Rightarrow S = \frac{1}{2}ac.\frac{{\sqrt 2 }}{2} = \frac{{\sqrt 2 }}{4}.ac\)
Chọn D

Ta có:
\(E=\left\{x\in R|x< -3\right\}\)
\(\Rightarrow E=\left\{....;-3\right\}\)
\(\Rightarrow E=\left\{-3;-\infty\right\}\)
Vậy chọn C

Ta có
A B → = 1 ; 7 ⇒ A B = 1 2 + 7 2 = 5 2 B C → = − 7 ; 1 ⇒ B C = 5 2 C D → = − 1 ; − 7 ⇒ C D = 5 2 D A → = 7 ; − 1 ⇒ D A = 5 2 ⇒ A B = B C = C D = D A = 5 2 .
Lại có: A B → . B C → = 1 − 7 + 7.1 = 0 nên A B ⊥ B C .
Từ đó suy ra ABCD là hình vuông.
Chọn C.

Đáp án D
Ta có thể thấy ngay rằng các khẳng định A và C đều đúng.
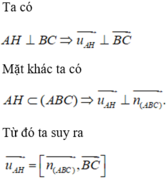
là một vectơ chỉ phương của đường thẳng AH.
Vậy D là khẳng định sai.

Đáp án D
Ta có:
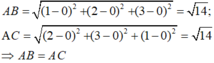
Ta thấy tam giác ABC cân tại đỉnh A. Do đó, AD đồng thời là đường cao của tam giác ABC nên các khẳng định A, B và C đều đúng.
Vậy khẳng định D sai.

Chọn D. Đây là một tính chất của tích vô hướng.
A. Sai vì \(({\overrightarrow a .\overrightarrow b})\overrightarrow c = [ {|\overrightarrow a |.|\overrightarrow b |\;\,\cos ( {\overrightarrow a ,\overrightarrow b } )} ].\overrightarrow c \ne \)\(\overrightarrow a \,\,( {\overrightarrow b .\overrightarrow c }) = \overrightarrow a \,\,[ {|\overrightarrow b |.|\overrightarrow c |\;\,\cos ( {\overrightarrow b ,\overrightarrow c })}]\)
B. Sai vì \((\overrightarrow a .\overrightarrow b)^2 = {[{\overrightarrow a .\overrightarrow b = | {\overrightarrow a } |.| {\overrightarrow b }|\,\cos ( {\overrightarrow a ,\overrightarrow b })}]^2} = {\overrightarrow a ^2}\,.\,{\overrightarrow b ^2}.{\cos ^2}( {\overrightarrow a ,\overrightarrow b } )\)\( \ne \;\;{\overrightarrow a ^2}\,.\,{\overrightarrow b ^2}\)
C. Sai vì \(\overrightarrow a .\overrightarrow b = | {\overrightarrow a }|.| {\overrightarrow b } |\,\cos ( {\overrightarrow a ,\overrightarrow b }) \ne | {\overrightarrow a }|.| {\overrightarrow b }|\,\sin ( {\overrightarrow a ,\overrightarrow b })\)


A sai khi c ≤ 0; B sai, chẳng hạn khi a < 0 < b; C sai chẳng hạn khi a < b < 0.
Đáp án: D