Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo định lí sin, ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
=> \(R = \frac{a}{{2\sin A}}\) => A sai.
\(R = \frac{b}{{2\sin B}}=\frac{b}{{2\sin 135^o}}=\frac{{\sqrt 2 }}{2}b\) => B đúng.
C. \(R = \frac{{\sqrt 2 }}{2}c\) (Loại vì không có dữ kiện về góc C nên không thể tính R theo c.)
D. \(R = \frac{{\sqrt 2 }}{2}a\) (Loại vì không có dữ kiện về góc A nên không thể tính R theo a.)
Chọn B

A. \({a^2} = {b^2} + {c^2} + \sqrt 2 ab.\) (Loại)
Vì: Theo định lí cos ta có: \({a^2} = {b^2} + {c^2} - 2bc.\cos A\)
Không đủ dữ kiện để suy ra \({a^2} = {b^2} + {c^2} + \sqrt 2 ab.\)
B. \(\frac{b}{{\sin A}} = \frac{a}{{\sin B}}\) (Loại)
Theo định lí sin, ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} \nRightarrow \frac{b}{{\sin A}} = \frac{a}{{\sin B}}\)
C. \(\sin B = \frac{{ - \sqrt 2 }}{2}\)(sai vì theo câu a, \(\sin B = \frac{{\sqrt 2 }}{2}\))
D. \({b^2} = {c^2} + {a^2} - 2ca\cos {135^o}.\)
Theo định lý cos ta có:
\({b^2} = {c^2} + {a^2} - 2ca.\cos B\) (*)
Mà \(\widehat B = {135^o} \Rightarrow \cos B = \cos {135^o}\).
Thay vào (*) ta được: \({b^2} = {c^2} + {a^2} - 2ca\;\cos {135^o}\)
=> D đúng.
Chọn D

Áp dụng định lí cosin trong tam giác ABC ta có:
\({a^2} = {b^2} + {c^2} - 2bc.\cos A\)\( \Rightarrow \cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)
Mà \(\sin A = \sqrt {1 - {{\cos }^2}A} \).
\( \Rightarrow \sin A = \sqrt {1 - {{\left( {\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}} \right)}^2}} = \sqrt {\frac{{{{(2bc)}^2} - {{({b^2} + {c^2} - {a^2})}^2}}}{{{{(2bc)}^2}}}} \)
\( \Leftrightarrow \sin A = \frac{1}{{2bc}}\sqrt {{{(2bc)}^2} - {{({b^2} + {c^2} - {a^2})}^2}} \)
Đặt \(M = \sqrt {{{(2bc)}^2} - {{({b^2} + {c^2} - {a^2})}^2}} \)
\(\begin{array}{l} \Leftrightarrow M = \sqrt {(2bc + {b^2} + {c^2} - {a^2})(2bc - {b^2} - {c^2} + {a^2})} \\ \Leftrightarrow M = \sqrt {\left[ {{{(b + c)}^2} - {a^2}} \right].\left[ {{a^2} - {{(b - c)}^2}} \right]} \\ \Leftrightarrow M = \sqrt {(b + c - a)(b + c + a)(a - b + c)(a + b - c)} \end{array}\)
Ta có: \(a + b + c = 2p\)\( \Rightarrow \left\{ \begin{array}{l}b + c - a = 2p - 2a = 2(p - a)\\a - b + c = 2p - 2b = 2(p - b)\\a + b - c = 2p - 2c = 2(p - c)\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow M = \sqrt {2(p - a).2p.2(p - b).2(p - c)} \\ \Leftrightarrow M = 4\sqrt {(p - a).p.(p - b).(p - c)} \\ \Rightarrow \sin A = \frac{1}{{2bc}}.4\sqrt {p(p - a)(p - b)(p - c)} \\ \Leftrightarrow \sin A = \frac{2}{{bc}}.\sqrt {p(p - a)(p - b)(p - c)} \end{array}\)
b) Ta có: \(S = \frac{1}{2}bc\sin A\)
Mà \(\sin A = \frac{2}{{bc}}\sqrt {p(p - a)(p - b)(p - c)} \)
\(\begin{array}{l} \Rightarrow S = \frac{1}{2}bc.\left( {\frac{2}{{bc}}\sqrt {p(p - a)(p - b)(p - c)} } \right)\\ \Leftrightarrow S = \sqrt {p(p - a)(p - b)(p - c)} .\end{array}\)

a) Chọn đáp án B
A. \(S = \frac{{abc}}{{4r}}\)
Ta có: \(S = \frac{{abc}}{{4R}}\). Mà \(r < R\)nên suy ra \(S = \frac{{abc}}{{4R}} < \frac{{abc}}{{4r}}\)
Vậy A sai.
B. \(r = \frac{{2S}}{{a + b + c}}\)
Ta có: \(S = pr \Rightarrow r = \frac{S}{p}\)
Mà\(p = \frac{{a + b + c}}{2}\;\; \Rightarrow r = \frac{S}{p}\; = \frac{S}{{\frac{{a + b + c}}{2}}} = \frac{{2S}}{{a + b + c}}\;\)
Vậy B đúng
C. \({a^2} = {b^2} + {c^2} + 2bc\;\cos A\)
Sai vì theo định lí cos ta có: \({a^2} = {b^2} + {c^2} - 2bc\;\cos A\)
D. \(S = r\,(a + b + c)\)
Sai vì \(S = pr = r.\frac{{a + b + c}}{2}\)
b) Chọn đáp án A
A. \(\sin A = \sin \,(B + C)\)
Ta có: \(\widehat A + \widehat B + \widehat C = {180^o}\)
\(\begin{array}{l} \Rightarrow \widehat B + \widehat C = {180^o} - \widehat A\\ \Rightarrow \sin \,(B + C) = \sin A\end{array}\)
Vậy A đúng.
B. \(\cos A = \cos \,(B + C)\)
Sai vì \(\cos \,(B + C) = - \cos A\)(Do \(\widehat A + \widehat B + \widehat C = {180^o}\))
C. \(\;\cos A > 0\)
Không đủ dữ kiện để kết luận.
Nếu \({0^o} < \widehat A < {90^o}\) thì \(\cos A > 0\)
Nếu \({90^o} < \widehat A < {180^o}\) thì \(\cos A < 0\)
D. \(\sin A\,\, \le 0\)
Ta có \(S = \frac{1}{2}bc.\sin A > 0\)
Mà \(b,c > 0\)
\( \Rightarrow \sin A > 0\)
Vậy D sai.

Lời giải:
Ta có:
$a+b+c=abc\Rightarrow a(a+b+c)=a^2bc$
$\Leftrightarrow bc+a(a+b+c)=bc(a^2+1)$
$\Leftrightarrow (a+b)(a+c)=bc(a^2+1)$
$\Rightarrow \frac{a}{\sqrt{bc(a^2+1)}}=\frac{a}{\sqrt{(a+b)(a+c)}}$
Áp dụng BĐT AM-GM:
\(\frac{a}{\sqrt{bc(1+a^2)}}=\frac{a}{\sqrt{(a+b)(a+c)}}\leq \frac{1}{2}\left(\frac{a}{a+b}+\frac{a}{a+c}\right)\)
Hoàn toàn tương tự với các phân thức còn lại:
\(S\leq \frac{1}{2}\left(\frac{a}{a+b}+\frac{a}{a+c}+\frac{b}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}+\frac{c}{c+b}\right)=\frac{3}{2}\)
Vậy $S_{\max}=\frac{3}{2}$. Dấu "=" xảy ra khi $a=b=c=\sqrt{3}$

Bài 1. Ta có: \(a\left(a+2\right)\left(a-1\right)^2\ge0\therefore\frac{1}{4a^2-2a+1}\ge\frac{1}{a^4+a^2+1}\)
Thiết lập tương tự 2 BĐT còn lại và cộng theo vế rồi dùng Vasc (https://olm.vn/hoi-dap/detail/255345443802.html)
Bài 5: Bất đẳng thức này đúng với mọi a, b, c là các số thực. Chứng minh:
Quy đồng và chú ý các mẫu thức đều không âm, ta cần chứng minh:
\(\frac{1}{2}\left(a^2+b^2+c^2-ab-bc-ca\right)\Sigma\left[\left(a^2+b^2\right)+2c^2\right]\left(a-b\right)^2\ge0\)
Đây là điều hiển nhiên.

4.
\(\frac{a^3}{b}+\frac{b^3}{c}+\frac{c^3}{a}=\frac{a^4}{ab}+\frac{b^4}{bc}+\frac{c^4}{ac}\ge\frac{\left(a^2+b^2+c^2\right)}{ab+bc+ca}\)
\(\Rightarrow\frac{a^3}{b}+\frac{b^3}{c}+\frac{c^3}{a}\ge\frac{\left(ab+bc+ca\right)^2}{ab+bc+ca}=ab+bc+ca\)
Dấu "=" xảy ra khi \(a=b=c\)
5.
\(\frac{a}{bc}+\frac{b}{ca}\ge2\sqrt{\frac{ab}{bc.ca}}=\frac{2}{c}\) ; \(\frac{a}{bc}+\frac{c}{ab}\ge\frac{2}{b}\) ; \(\frac{b}{ca}+\frac{c}{ab}\ge\frac{2}{a}\)
Cộng vế với vế:
\(2\left(\frac{a}{bc}+\frac{b}{ca}+\frac{c}{ab}\right)\ge2\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
\(\Rightarrow\frac{a}{bc}+\frac{b}{ca}+\frac{c}{ab}\ge\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)
1.
Áp dụng BĐT \(x^2+y^2+z^2\ge xy+yz+zx\)
\(\Rightarrow\left(\sqrt{ab}\right)^2+\left(\sqrt{bc}\right)^2+\left(\sqrt{ca}\right)^2\ge\sqrt{ab}.\sqrt{bc}+\sqrt{ab}.\sqrt{ac}+\sqrt{bc}.\sqrt{ac}\)
\(\Rightarrow ab+bc+ca\ge\sqrt{abc}\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)\)
2.
\(\frac{ab}{c}+\frac{bc}{a}\ge2\sqrt[]{\frac{ab.bc}{ca}}=2b\) ; \(\frac{ab}{c}+\frac{ac}{b}\ge2a\) ; \(\frac{bc}{a}+\frac{ac}{b}\ge2c\)
Cộng vế với vế:
\(2\left(\frac{ab}{c}+\frac{bc}{a}+\frac{ac}{b}\right)\ge2\left(a+b+c\right)\)
\(\Leftrightarrow\frac{ab}{c}+\frac{bc}{a}+\frac{ac}{b}\ge a+b+c\)
3.
Từ câu b, thay \(c=1\) ta được:
\(ab+\frac{b}{a}+\frac{a}{b}\ge a+b+1\)

Hình như đề bài có vấn đề : thừa đk ab + bc + ac = abc
ta có : \(\frac{\sqrt{b^2+2a^2}}{ab}\ge\frac{\sqrt{4a^2b^2}}{ab}=\frac{2ab}{ab}=2\)
Tương tự \(\frac{\sqrt{c^2+2b^2}}{bc}\ge2\) ; \(\frac{\sqrt{a^2+2c^2}}{ac}\ge2\)
\(\Rightarrow\frac{\sqrt{b^2+2a^2}}{ab}+\frac{\sqrt{c^2+2b^2}}{bc}+\frac{\sqrt{a^2+2c^2}}{ac}\ge2+2+2=6>\sqrt{3}\)
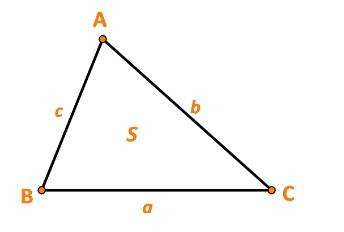

Diện tích tam giác ABC: \(S = \frac{1}{2}ac.\sin B\)
Mà \(\widehat B = {135^o} \Rightarrow \sin B = \sin {135^o} = \frac{{\sqrt 2 }}{2}\).
\( \Rightarrow S = \frac{1}{2}ac.\frac{{\sqrt 2 }}{2} = \frac{{\sqrt 2 }}{4}.ac\)
Chọn D