
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a, \(\dfrac{2}{3}\) + \(\dfrac{1}{5}\). \(\dfrac{10}{7}\)
= \(\dfrac{2}{3}\) + \(\dfrac{2}{7}\)
= \(\dfrac{20}{21}\)
b, \(\dfrac{7}{12}\) - \(\dfrac{27}{7}\). \(\dfrac{1}{18}\)
= \(\dfrac{7}{12}\) - \(\dfrac{3}{14}\)
= \(\dfrac{31}{84}\)
c, \(\dfrac{3}{10}\). \(\dfrac{-5}{6}\) - \(\dfrac{1}{8}\)
= - \(\dfrac{1}{4}\) - \(\dfrac{1}{8}\)
= - \(\dfrac{3}{8}\)
d, - \(\dfrac{4}{9}\): \(\dfrac{8}{3}\) + \(\dfrac{1}{18}\)
= - \(\dfrac{1}{6}\) + \(\dfrac{1}{18}\)
= - \(\dfrac{1}{9}\)
e, {[(\(\dfrac{1}{2}\) - \(\dfrac{2}{3}\))2 : 2 ] - 1}. \(\dfrac{4}{5}\)
= {[ (-\(\dfrac{1}{6}\))2 : 2] - 1}. \(\dfrac{4}{5}\)
= { [\(\dfrac{1}{36}\) : 2] - 1}. \(\dfrac{4}{5}\)
= { \(\dfrac{1}{72}\) - 1}. \(\dfrac{4}{5}\)
=- \(\dfrac{71}{72}\).\(\dfrac{4}{5}\)
= -\(\dfrac{71}{90}\)



Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)

B1: c/m A chia hết cho 10
B2: c/m A chia hết cho 13
Kết hợp với (10;13)=1=> A chia hết cho 130

Áp dụng tc dtsbn:
\(\dfrac{2y+z-x}{x}=\dfrac{2z-y+x}{y}=\dfrac{2x+y-z}{z}=\dfrac{2x+2y+2z}{x+y+z}=\dfrac{2\left(x+y+z\right)}{x+y+z}=2\\ \Rightarrow\left\{{}\begin{matrix}2y+z-x=2x\\2z-y+x=2y\\2x+y-z=2z\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}2y+z=3x\\2z+x=3y\\2x+y=3z\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3x-2y=z\\3y-2z=x\\3z-2x=y\end{matrix}\right.;\left\{{}\begin{matrix}3x-z=2y\\3y-x=2z\\3z-y=2z\end{matrix}\right.\\ \Rightarrow P=\dfrac{xyz}{2x\cdot2y\cdot2z}=\dfrac{1}{8}\)
Chọn D



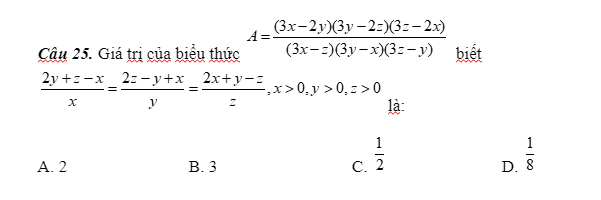
Chọn B
um cho e cách giải luôn ạ...