Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

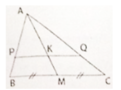
Ta có:
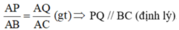
Vì K ∈ PQ nên PK // BM; KQ // MC
Trong ΔABM có PK // BM nên
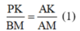
Trong ΔAMC có KQ // MC nên
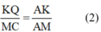
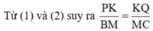
mà BM = MC (gt) nên PK = KQ.

Từ B và C kẻ 2 đường thẳng song song với d, chúng cắt AM lần lượt tại H và K.
Theo ĐL Thales, ta có: \(\frac{AB}{AD}=\frac{AH}{AO}\)\(;\frac{AC}{AE}=\frac{AK}{AO}\)
\(\Rightarrow\frac{AB}{AD}+\frac{AC}{AE}=\frac{AH+AK}{AO}\)
Tam giác BHM= Tam giác CKM (g.c.g) => HM=KM
\(\Rightarrow AH+AK=AH+AH+HM+KM=2AH+2HM=2AM\)
\(\Rightarrow\frac{AB}{AD}+\frac{AC}{AE}=\frac{2AM}{AO}\)
Do O là trung điểm AM nên \(\frac{AB}{AD}+\frac{AC}{AE}=\frac{4AO}{AO}=4\)(đpcm).

Xét tam giác ABC có: \(\frac{AP}{AB}=\frac{AQ}{AC}\left(gt\right)\)
\(\Rightarrow PQ//BC\)( Định lý Ta-let đảo )
Xét tam giác ABM có PK//BM ( PQ//BC )
\(\Rightarrow\frac{PK}{BM}=\frac{AK}{AM}\)( hệ quả của định lý Ta-let ) (1)
Xét tam giác AMC có KQ//MC ( PQ//BC )
\(\Rightarrow\frac{KQ}{MC}=\frac{AK}{AM}\)( hệ quả của định lý Ta-let ) (2)
Mà BM=MC ( vì AM là đường trung tuyến úng với BC ) (3)
Từ (1),(2) và (3) \(\Rightarrow KQ=KP\left(đpcm\right)\)

a) Xét \(\Delta\)ABD có: ME // AD
=> \(\frac{BM}{BD}=\frac{EM}{AD}\)(1)
Xét \(\Delta\)CFM có: AD//FM
=> \(\frac{AD}{FM}=\frac{CD}{CM}\)=> \(\frac{CM}{CD}=\frac{FM}{AD}\)(2)
Từ (1); (2) => \(\frac{EM}{AD}+\frac{FM}{AD}=\frac{BM}{BD}+\frac{CM}{CD}\)vì AD là trung tuyến => BD = CD
=> \(\frac{EM+FM}{AD}=\frac{BM+CM}{CD}=\frac{BC}{CD}=2\)
=> \(EM+FM=2AD\)
b) Tứ giác ADMI là hình bình hành
Chứng minh:
I là trung điểm của EF
=> ME + MF = ME + ME + EF = 2ME + 2EI = 2( ME + EI ) = 2MI
mà ME + MF = 2 AD
=> MI = AD
Mặt khác: MI//AD
=> ADMI là hình bình hành