Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


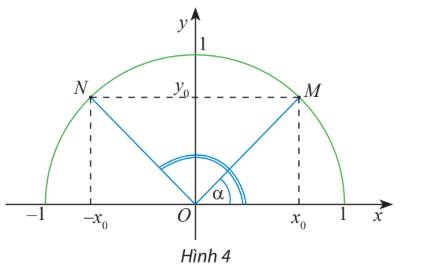
a) Do MN song song với Ox nên \(\alpha = \widehat {OMN} = \widehat {ONM} = \widehat {NOx'}\)
Mà \(\widehat {xON} = {180^o} - \widehat {NOx'} = {180^o} - \alpha \)
\( \Rightarrow \widehat {xON} = {180^o} - \alpha \)
b) Dễ thấy: Điểm N đối xứng với M qua trục Oy
\( \Rightarrow N( - {x_0};{y_0})\)
Lại có: điểm N biểu diễn góc \({180^o} - \alpha \)
\( \Rightarrow \left\{ \begin{array}{l}\sin ({180^o} - \alpha ) = {y_N} = {y_0}\\\cos ({180^o} - \alpha ) = {x_N} = - {x_0}\end{array} \right.\);
Mà: \(\sin \alpha = {y_0};\;\cos \alpha = {x_0}\)
\( \Rightarrow \left\{ \begin{array}{l}\sin ({180^o} - \alpha ) = \sin \alpha \;\\\cos ({180^o} - \alpha ) = - \cos \alpha \end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}\tan ({180^o} - \alpha ) = - \tan \alpha \;\\\cot ({180^o} - \alpha ) = - \cot \alpha \end{array} \right.\)

Tham khảo:
Trường hợp 1: \(\alpha = {90^o}\)
Khi đó \({90^o} - \alpha = {0^o}\)
Tức là M và N lần lượt trùng nhau với B và A.
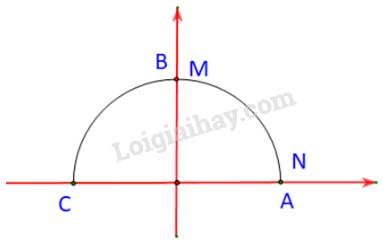
Và \(\cos \alpha = 0 = \sin \left( {{{90}^o} - \alpha } \right)\)
Trường hợp 2: \({0^o} < \alpha < {90^o} \Rightarrow {0^o} < {90^o} - \alpha < {90^0}\)
M và N cùng nằm bên trái phải trục tung.
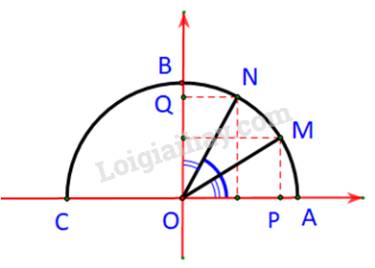
Ta có: \(\alpha = \widehat {AOM};\;\;{90^o} - \alpha = \widehat {AON}\)
Dễ thấy: \(\widehat {AON} = {90^o} - \alpha = {90^o} - \widehat {NOB}\;\;\; \Rightarrow \alpha = \widehat {NOB}\)
Xét hai tam giác vuông \(NOQ\) và tam giác \(MOP\) ta có:
\(OM = ON\)
\(\widehat {POM} = \widehat {QON}\)
\(\begin{array}{l} \Rightarrow \Delta NOQ = \Delta MOP\\ \Rightarrow \left\{ \begin{array}{l}OP = OQ\\QN = MP\end{array} \right.\end{array}\)
Mà \(M\left( {{x_0};{y_o}} \right)\) nên \(N\left( {{y_o};{x_0}} \right)\). Nói cách khác:
\(\cos \left( {{{90}^o} - \alpha } \right) = \sin \alpha ;\;\;\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha .\)

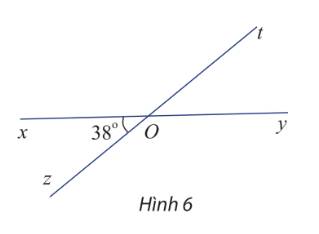
Ta có hai góc \(\widehat {xOz}\) và \(\widehat {tOy}\) đối đỉnh nên \(\widehat {xOz} = \widehat {tOy} = 38^\circ \)
hai góc \(\widehat {xOt}\) và \(\widehat {yOz}\) đối đỉnh nên \(\widehat {xOt} = \widehat {yOz}\)
\(\widehat {xOz}\) và \(\widehat {xOt}\) bù nhau nên \(\widehat {xOt} = 180^\circ - \widehat {xOz} = 180^\circ - 38^\circ = 142^\circ \)
Vậy \(\widehat {xOz} = \widehat {tOy} = 38^\circ \) và \(\widehat {xOt} = \widehat {yOz} = 142^\circ \)

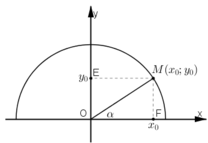
Gọi E, F lần lượt là hình chiếu của M trên Oy, Ox.
Khi đó xét ΔMOF vuông tại F thì :
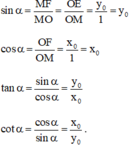

Đáp án C
Đường tròn (C) có tâm I( -1 ; 3) và bán kính R= 2
Do d’// d nên phương trình của d’ có dạng : 3x- 4y + c= 0.
Để d’ chắn trên (C) một dây cung có độ dài lớn nhất thì d’ phải đi qua tâm I của đường tròn ( trong các dây của đường tròn dây lớn nhất là đường kính).
Do I( -1 ; 3) thuộc d’ nên : 3.(-1) – 4.3 +c= 0
=> c = 15
Vậy đường thẳng cần tìm là d’ : 3x- 4y + 15= 0.

a) Áp dụng định lí cosin trong tam giác ABC, ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\\ \Leftrightarrow B{C^2} = {3^2} + {4^2} - 2.3.4.\cos {120^o}\\ \Leftrightarrow B{C^2} = 37\\ \Leftrightarrow BC \approx 6\end{array}\)
Áp dụng định lí sin trong tam giác ABC, ta có:
\(\begin{array}{l}\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = 2R\\ \Rightarrow \sin B = \frac{{AC.\sin A}}{{BC}} = \frac{{4.\sin {{120}^o}}}{6} = \frac{{\sqrt 3 }}{3}\\ \Leftrightarrow \widehat B \approx {35^o}\end{array}\)
b) \(R = \frac{{BC}}{{2.\sin A}} = \frac{6}{{2.\sin {{120}^o}}} = 2\sqrt 3 \)
c) Diện tích tam giác ABC: \(S = \frac{1}{2}4.3.\sin {120^o} = 3\sqrt 3 .\)
d) Gọi H là chân đường cao hạ từ đỉnh A.
Ta có: \(S = \frac{1}{2}AH.BC\)
\( \Rightarrow AH = \frac{{2S}}{{BC}} = \frac{{2.3\sqrt 3 }}{6} = \sqrt 3 \)
e) \(\overrightarrow {AB} .\overrightarrow {AC} = 3.4.\cos (\widehat {BAC}) = 12.\cos {120^o} = - 6.\)
Ta có: \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \) (do M là trung điểm BC)
\( \Leftrightarrow \overrightarrow {AM} = \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {AC} )\)
\(\begin{array}{l} \Rightarrow \overrightarrow {AM} .\overrightarrow {BC} = \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {AC} )(\overrightarrow {AC} - \overrightarrow {AB} )\\ = \frac{1}{2}\left( {{{\overrightarrow {AC} }^2} - {{\overrightarrow {AB} }^2}} \right) = \frac{1}{2}\left( {A{C^2} - A{B^2}} \right)\\ = \frac{1}{2}\left( {{4^2} - {3^2}} \right) = \frac{7}{2}.\end{array}\)

Đáp án B
Đường tròn (C) có tâm I( 1; -3) và R= 2
![]() có phương trình 4x- 3y+ m= 0.
có phương trình 4x- 3y+ m= 0.
Vẽ
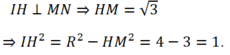
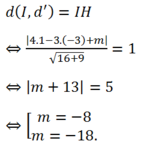

Vậy:
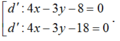

Tham khảo:
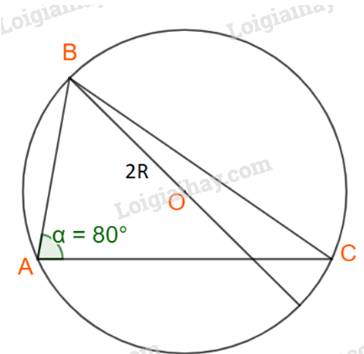
Áp dụng định lí sin cho tam giác ABC ta có:
\(\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = 2R\)
\(\begin{array}{l} \Rightarrow \sin C = \frac{{c.\sin B}}{b} = \frac{{5.\sin {{80}^o}}}{8} \approx 0,6155\\ \Leftrightarrow \widehat C \approx {38^o}\end{array}\)
Lại có: \(\widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {80^o} - {38^o} = {62^o}\)
Theo định lí sin, ta suy ra \(a = \sin A.\dfrac{b}{{\sin B}} = \sin {62^o}\dfrac{8}{{\sin {{80}^o}}} \approx 7,17\)
Và \(2R = \dfrac{b}{{\sin B}} \Rightarrow R = \dfrac{b}{{2\sin B}} = \dfrac{8}{{2\sin {{80}^o}}} \approx 4,062.\)
Vậy tam giác ABC có \(\widehat A = {62^o}\); \(\widehat C \approx {38^o}\); \(a \approx 7,17\) và \(R \approx 4,062.\)
Gọi H là hình chiếu vuông góc của N Ox.
Ta có: \(\widehat {NOH} = \widehat {ONM} = \widehat {OMN} = \widehat {MOx} = \alpha \) (do NM song song với Ox)
Mà \(\widehat {xOM} + \widehat {NOH} = {180^o}\)
Suy ra \(\widehat {xON} + \widehat {MOx} = {180^o}\)