

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



+ Giả sử phương trình truyền sóng ở hai nguồn u = acosꞷt
+ Xét điểm N trên CO: AN = BN = d; ON = x với 0 ≤ x ≤ 8 c m
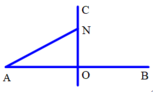
+ Biểu thức sóng tại N: u N = 2 a cos ω t − 2 π d λ
+ Để uN dao động ngược pha với hai nguồn: 2 π d λ = 2 k = 1 π ⇒ d = k + 1 2 λ = 1 , 6 k + 0 , 8
+ Ta có: d 2 = A O 2 + x 2 = 6 2 + x 2 ⇒ 1 , 6 k + 0 , 8 2 = 36 + x 2 ⇒ 0 ≤ x 2 = 1 , 6 k + 0 , 8 2 − 36 ≤ 64
⇒ 6 ≤ 1 , 6 k + 0 , 8 ≤ 10 ⇒ 4 ≤ k ≤ 5
→ Có 2 giá trị của k: 4, 5 nên có hai vị trí dao động ngược pha với nguồn
Chọn đáp án D

Chọn đáp án D
Giả sử phương trình truyền sóng ở hai nguồn u = acost
Xét điểm N trên CO: AN = BN = d; ON = x với 0 ≤ x ≤ 8 c m
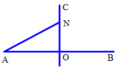
Biểu thức sóng tại N:
u
N
=
2
a
cos
ω
t
−
2
π
d
λ
Để uN dao động ngược pha với hai nguồn:
2 π d λ = 2 k = 1 π ⇒ d = k + 1 2 λ = 1 , 6 k + 0 , 8
Ta có:
d 2 = A O 2 + x 2 = 6 2 + x 2 ⇒ 1 , 6 k + 0 , 8 2 = 36 + x 2 ⇒ 0 ≤ x 2 = 1 , 6 k + 0 , 8 2 − 36 ≤ 64
⇒ 6 ≤ 1 , 6 k + 0 , 8 ≤ 10 ⇒ 4 ≤ k ≤ 5
→ Có 2 giá trị của k: 4, 5 nên có hai vị trí dao động ngược pha với nguồn

Đáp án B
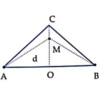
- Xét trên tam giác vuông AOC có OA = 6 cm, OC = 8 cm → AC = 8 2 + 6 2 = 10cm.
- Gọi M là điểm nằm trên CO dao động cùng pha với nguồn → AM = kλ = 1,6k.
Lại có AO ≤ AM ≤ AC ↔ 6 ≤ 1,6k ≤ 10 → 3,75 ≤ k ≤ 6,75
Có 3 giá trị k nguyên thỏa mãn → Trên CO có 3 điểm dao động cùng pha với nguồn.
- Trên đoạn DO (với D đối xứng với C qua O) cũng có 3 điểm dao động cùng pha với nguồn.
→ Trên CD có tất cả có 6 điểm dao động cùng pha với nguồn.

Chọn đáp án B
Xét tam giác vuông AOC có OA = 6 cm và OC = 8 cm → AC =10 cm.
- Gọi M là điểm nằm trên đoạn CO và dao động cùng pha với nguồn → AM = kλ = 1,6k.
A O ≤ A M ≤ A C → 6 ≤ 1,6 k ≤ 10 → 3,75 ≤ k ≤ 6,75
Có 3 giá trị k nguyên thỏa mãn → có 3 điểm trên đoạn CO dao động cùng pha với nguồn.
- Tương tự trên đoạn DO cũng có 3 điểm dao động cùng pha với nguồn.
→ Có 6 điểm trên đoạn CD dao động cùng pha với nguồn.

Đáp án B
Xét tam giác vuông AOC có OA = 6 cm và OC = 8 cm → AC =10 cm.
- Gọi M là điểm nằm trên đoạn CO và dao động cùng pha với nguồn → AM = kλ = 1,6k.
A O ≤ A M ≤ A C → 6 ≤ 1 , 6 k ≤ 10 → 3 , 75 ≤ k ≤ 6 , 75
Có 3 giá trị k nguyên thỏa mãn → có 3 điểm trên đoạn CO dao động cùng pha với nguồn.
- Tương tự trên đoạn DO cũng có 3 điểm dao động cùng pha với nguồn.
→ Có 6 điểm trên đoạn CD dao động cùng pha với nguồn.


Sóng tại N ngược pha với sóng tại hai nguồn khi
Δ
φ
=
π
+
2
k
π
⇒
d
=
λ
2
+
k
λ
=
0
,
8
+
1
,
6
k
A
O
≤
d
≤
A
C
⇒
6
≤
d
≤
10
⇒
3
,
25
≤
k
≤
5
,
75
→Có hai điểm dao động ngược pha với nguồn trên đoạn CO

Đáp án D
Hai nguồn giống nhau có thể coi cùng phương trình u A = u B = A cos ω t
Phương trình 2 sóng thành phần tại M là 1 điểm bất kì trên đoạn CO
u A M = A cos ( ω t - 2 π λ d 1 ) , u B M = A cos ( ω t - 2 π λ d 2 ) . Chú ý ( d 1 = d 2 = d )
Phương trình sóng tổng hợp tại M: u M = u A M + u B M = 2 A cos ( ω t - 2 π λ d )
Để sóng tại M ngược pha với hai nguồn thì 2 π λ d = ( 2 k + 1 ) π ⇒ d = ( 2 k + 1 ) λ 2
Do M nằm trên đoạn CO nên d có điều kiện: 6 c m ≤ d ≤ 6 2 + 8 2 = 10cm. Hay 3 , 25 ≤ k ≤ 5 , 75 ⇒ k = 4 , 5 .
Vậy có 2 điểm thỏa mãn.

Đáp án B
Phương trình dao động của hai nguồn ![]()
Phương trình dao động của điểm M thuộc CO, cách nguồn khoảng d là:
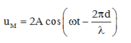
Vì điểm M dao động ngược pha với nguồn nên:
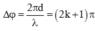
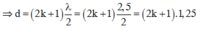
Mà ![]()
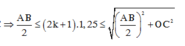
![]()
![]()
Vậy trên đoạn CO có 1 điểm dao động ngược pha với nguồn.

Độ lệch pha giữa điểm P bất kỳ trên CO với nguồn A hoặc B là
\(\Delta \varphi = \frac{2\pi d}{\lambda} \), d là khoảng cách từ điểm đó đến mỗi nguồn.
P ngược pha với hai nguồn tức là \(\Delta \varphi = (2k+1)\pi => d = (k+\frac{1}{2}) \lambda.\)
Số điểm dao động ngược pha với nguồn trên CO là
\(-d_0 < d \leq d_1\)
=> \(-d_0 < (k+\frac{1}{2})\lambda < d_1\)
=> \(-6 < (k+0,5)1,6 \leq 10.\) ( do \(d_1 = \sqrt{6^2+8^2} = 10cm.\))
=> \(-4,25 < k < 5,75.\)
=> \(k = -4,...5\)
Như vậy số giá trị của k là 10.
Số điểm dao động ngược pha với nguồn là 10 điểm.
Chú ý là bài này mình đã cho là hai nguồn đồng pha.