

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án A
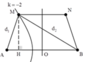
Số điểm dao động với biên độ cực đại trên AB
- A B λ ≤ k ≤ A B λ ⇔ - 8 ≤ k ≤ 8
Để diện tích AMNB là lớn nhất thì M phải nằm trên cực đại ứng với k=-2
d 1 - d 2 = - 2 k λ = - 2 c m .
Mặc khác d 1 2 = A H 2 + M H 2 d 2 2 = B H 2 + M H 2 ⇒ d 1 + d 2 = B H 2 - A H 2 2 = 16 c m
Ta tính được d 1 = 7 c m từ đó suy ra M H = 2 5 c m .
Diện tích hình thang S A M N B = 1 2 A B + M N M H = 18 5 c m 2 .

Chọn D
Hai nguồn A, B cùng pha
ðĐể giữa hai điểm CD có cực đại thì giữa A và B cũng chỉ có đúng 3 đường cực đại thì k nhận các giá trị -1,0,1. Nghĩa là phải có vân cực đại bậc 1 vân bậc 2 phải nằm ngoài.
ðCA-CB£kl£DA-DB
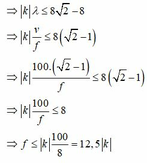
=> với k =1 thì f=12,5Hz
Với k=2 thì f=25Hz
=> phải nhỏ hơn 25Hz để không có vân bậc 2 trong khoảng CD và f phải lớn hơn hoặc bằng 12,5 Hz để có đủ 3 vân cực đại.

Đáp án B
Gọi khoảng cách từ một điểm bất kỳ thuộc CD đến các nguồn A, B tương ứng là d 2 và d 1
Ta có AD − BD ≤ d 2 − d 1 ≤ AC − BC
+ Điểm cực đại trên đoạn CD thỏa mãn: d 2 − d 1 = kλ, k = 0, ± 1, ± 2, ± 3 ... với ⇒ AD − BD ≤ kλ ≤ AC − BC ⇔ AD − BD λ ≤ k ≤ AC − BC λ
⇒ − 3 , 3 ≤ k ≤ 3 , 3
Có 7 giá trị của k là 0, ± 1, ± 2, ± 3 nên có 7 điểm cực đại trên CD
+ Điểm cực tiểu trên đoạn CD thỏa mãn: d 2 − d 1 = 2 k + 1 λ 2 , với k = 0, ± 1, ± 2, ± 3 ...
⇒ AD − BD ≤ 2 k + 1 λ 2 ≤ AC − BC ⇔ 2 AD − BD λ ≤ 2k + 1 ≤ 2 AC − BC λ ⇒ − 3 , 8 ≤ k ≤ − 2 , 83
Có 6 giá trị của k thỏa mãn k = 0, ± 1, ± 2, − 3 , − 2 nên có 6 điểm cực tiểu trên CD