Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hạnh ăn số táo là: 24. 25%=6 quả
số quả còn lại là: 24-6=18 quả
hoàng ăn số táo là: 18.4/9=8 quả
vậy trên đĩa còn: 18-8=10 quả.
Giải
Hạnh ăn số quả táo là : ( 24 : 100 ).25 = 6 (quả )
Trên đĩa còn lại số quả táo là : 24 - 6 =18 ( quả )
Hoàng ăn số quả táo là : ( 18 : 9 ).4 =8 ( quả )
Sau khi Hạnh và Hoàng ăn táo,thì trên đĩa còn lại số quả táo là : 24 - ( 6+8 ) =10 ( quả )
Đáp số : 10 quả

25 % số táo là :24 * 25% = 6 ( quả táo)
Số táo còn lại là : 24 - 6=18 (quả táo )
4/9 số táo còn lại là :18 * 4/9 = 8 (quả táo )
Trên dĩa còn số quả táo là :
18 - 8 = 10 (quả táo)

Bài giải
Số quả táo còn lại sau khi cô Mai cho bé Liên \(\frac{2}{3}\) số táo còn lại là: (không kể cô Mai cho bé Liên 1 quả táo)
1 + 9 = 10 (quả táo)
Phân số tương ứng với 10 quả táo là:
\(1-\frac{2}{3}=\frac{1}{3}\) (tương ứng với 10 quả táo)
Số quả táo còn lại sau khi cô Mai cho chị Linh là:
\(\frac{10\cdot3}{1}=30\) (quả táo)
Tương tự như thế, ta tính được số quả táo ban đầu cô Mai có tất cả là:
\(\left(30+2\right):\left(1-\frac{1}{3}\right)=48\) (quả táo)
Vậy, lúc đầu cô Mai có tất cả 48 quả táo.

Lan còn 10 quả táo vì Lan chỉ cho Mai 3 quả cam nên táo vẫn còn nguyên.

Gọi a là số táo ban đầu ở rổ 1
b là số táo ban đầu ở rổ 2
Lúc đầu số táo ở rổ 1 bằng 2/3 số táo ở rổ 2 nên ta có: a=\(\frac{2}{3}\)b (1)
Chuyển 32 quả táo từ rổ 2 sang rổ 1 thì số táo ở rổ 1 bằng 18/17 số táo ở rổ 2 nên ta có: (a+32)=\(\frac{18}{17}\)(b-32) (2)
Thế (1) vào (2) ta được: ( \(\frac{2}{3}\)b+32)=\(\frac{18}{17}\)(b-32)
<=> \(\frac{18}{17}\) b - \(\frac{2}{3}\)b = 32+\(\frac{576}{17}\)
<=> \(\frac{20}{51}\)b=\(\frac{1120}{17}\) <=> b=168Thế b=168 vào (1) suy ra a=112Vậy: Số táo ban đầu ở rổ 1 là 112 quả Số táo ban đầu ở rổ 2 là 168 quả

Nếu em có 15 quả táo thì tối đa em có thể cho anh 15 quả táo và thiếu 1 quả.
Vậy anh có 15 quả

Chọn đáp án C
Phương pháp
- Lập hệ bất phương trình ẩn x, y dựa vào điều kiện đề bài.
- Biểu diễn miền nghiệm của hệ trên mặt phẳng tọa độ.
- Tìm x, y để biểu thức tính số điểm M(x;y) đạt GTLN (tại một trong các điểm mút).
Cách giải
Gọi x, y lần lượt là số lít nước cam và nước táo mà mỗi đội cần pha chế (x≥0;y≥0)
Để pha chế x lít nước cam thì cần 30x (g) đường, x lít nước và x (g) hương liệu.
Để pha chế y lít nước táo thì cần 10y (g) đường, y lít nước và 4y (g) hương liệu.
Theo bài ra ta có hệ bất phương trình:
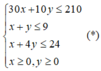
Số điểm đạt được khi pha x lít nước cam và y lít nước táo là: M(x;y)=60x+80y.
Bài toán trở thành tìm x, t thỏa để M(x;y) đạt GTLN.
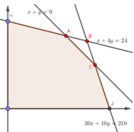
Ta biểu diễn miền nghiệm của (*) trên mặt phẳng tọa độ như sau:
Miền nghiệm là ngũ giác ACJIH
Tọa độ các giao điểm A(4;5),C(6;3),J(7;0),I(0;0),H(0;6).
M(x;y) sẽ đạt max, min tại các điểm đầu mút nên thay tọa độ từng giao điểm vào tính M(x;y) ta được:
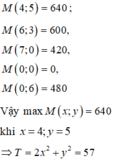
Số táo Hạnh đã ăn là :
24 x 25% = 6 ( quả)
Số táo Hoàng ăn là :
(24 - 6) x4/9 = 8 (quả)
Số táo còn trên đĩa là :
24 - (4 + 8) = 12 (quả)
Đáp số : 12 quả