Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
Tổng số điểm vừa lấy bằng: 3 + 4 + 5 + 6 = 18 (điểm).
Mỗi cách chọn ra 3 điểm không nằm trên một cạnh cho ta một tam giác.
Số cách chọn 3 điểm từ 18 điểm là: C 18 3 = 816(cách chọn).
Số cách chọn 3 điểm cùng nằm trên một cạnh là: 
(cách chọn).
Vậy số tam giác cần tìm bằng: 816 - 35 = 781(tam giác).
Chọn A
Phân tích.
- Ta thấy A thuộc đường phân giác trong góc A:x-3y+5=0 , giờ chỉ cần viết được phương trình AC là tìm được A.
- Trên AC đã có một điểm N, cần tìm thêm một điểm nữa. Chú ý khi lấy M’ đối xứng với M qua phân giác trong ta có M’ thuộc cạnh AC.
- Tìm M’ viết được phương trình AC từ đó suy ra A. Có A, M viết được phương trình AB.
- Gọi B, C và tham số hóa dựa vào B thuộc AB, C thuộc AC. Áp dụng công thức trọng tâm sẽ tìm ra được tọa độ B, C.
Có 2 trường hợp sau:
+ Lấy 1 điểm trên d1 và 2 điểm trên d2, suy ra cớ 10 C n 2 tam giác
+ Lấy 2 điểm trên d1 và 1 điểm trên d2, suy ra cớ n C 10 2 tam giác
Suy ra có
Đáp án B
Có 2 trường hợp sau:
+ Lấy 1 điểm trên d1 và 2 điểm trên d2, suy ra cớ 10 C n 2 tam giác
+ Lấy 2 điểm trên d1 và 1 điểm trên d2, suy ra cớ n C 10 2 tam giác
Suy ra có
Tham khảo:
+) \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là dãy số chu vi của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)
Ta có:
\({{\rm{p}}_2} = {p_{\Delta {A_1}{B_1}{C_1}}} = \frac{a}{2} + \frac{a}{2} + \frac{a}{2} = \frac{1}{2} \cdot (3a) = \frac{1}{2} \cdot {p_1}\)
\(\begin{array}{l}{{\rm{p}}_3} = {p_{\Delta {A_2}{B_2}{C_2}}} = \frac{a}{4} + \frac{a}{4} + \frac{a}{4} = {\left( {\frac{1}{2}} \right)^2} \cdot (3a) = {\left( {\frac{1}{2}} \right)^2} \cdot {p_1}\\ \ldots \\{p_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot {p_1}\\...\end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {p_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{2}} \right)}^{n - 1}} \cdot (3a)} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } (3a) = 0.3a = 0.\)
+)\(\left( {{{\rm{S}}_n}} \right)\) là dãy số diện tích của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)
Gọi \(h\) là chiều cao của tam giác \({\rm{ABC}}\) và \({\rm{h}} = \frac{{a\sqrt 3 }}{2}\).
Ta có:
\(\begin{array}{l}{{\rm{S}}_3} = {S_{\Delta {A_2}{B_2}{C_2}}} = \frac{1}{2} \cdot \frac{a}{4} \cdot \frac{h}{4} = {\left( {\frac{1}{4}} \right)^2} \cdot \left( {\frac{1}{2}ah} \right) = {\left( {\frac{1}{4}} \right)^2} \cdot {S_1}\\ \ldots \\{S_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot {S_1}\\ \ldots \end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {S_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{4}} \right)}^{n - 1}} \cdot {S_1}} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } \left( {\frac{1}{2}ah} \right) = 0 \cdot \frac{1}{2}ah = 0\).
b) +) Ta có \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{p}}_1}\) = 3a và công bội \({\rm{q}} = \frac{1}{2}\) thỏa mãn \(|q| < 1\) có tổng:
\({p_1} + {p_2} + \ldots + {p_n} + \ldots = \frac{{3a}}{{1 - \frac{1}{2}}} = 6a\)
+) Ta có \(\left( {{{\rm{S}}_n}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{S}}_1} = \frac{1}{2}ah\) và công bội \(q = \frac{1}{4}\) thỏa mãn \(|q| < 1\) có tổng:
\({S_1} + {S_2} + \ldots + {S_n} + \ldots = \frac{{\frac{1}{2}ah}}{{1 - \frac{1}{4}}} = \frac{2}{3}ah = \frac{2}{3}a.\frac{{a\sqrt 3 }}{2} = \frac{{{a^2}\sqrt 3 }}{3}\)
Chọn D
Lời giải. Số tam giác tạo thành có 3 đỉnh là 3 đỉnh của đa giác là C n 3
Số tam giác tạo thành có đúng 2 cạnh là cạnh của đa giác là n
Số tam giác tạo thành có đúng 1 cạnh là cạnh của đa giác là n(n-4)
(điều kiện n ∈ ℕ v à n < 4 )
→ số tam giác tạo thành không có cạnh nào là cạnh của đa giác là
Theo giả thiết, ta có
⇔ n = 35 ( t h ỏ a m ã n ) n = 4 ( l o ạ i )
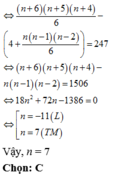
Chọn B
Lấy ba điểm phân biệt không thẳng hàng sẽ tạo thành một tam giác nên số tam giác tạo thành là: