

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
$\log(8.5^x+20^x)=x+\log 25$
$\Rightarrow 8.5^x+20^x=10^{x+\log 25}=10^x.25$
$\Rightarrow \frac{8.5^x+20^x}{10^x}=25$
$\Leftrightarrow \frac{8}{2^x}+2^x=25$
Đặt $2^x=t$ thì $\frac{8}{t}+t=25$
$\Leftrightarrow t^2-25t+8=0$
Dễ thấy PT trên luôn có 2 nghiệm dương $t_1,t_2$ nên kéo theo PT ban đầu có 2 nghiệm $x_1,x_2$
Tổng các nghiệm $x_1+x_2=\log_2(t_1)+\log_2(t_2)=\log_2(t_1t_2)=\log_2(8)=3$

1.a/ \(\left\{{}\begin{matrix}3^{x+1}>0\\5^{x^2}>0\end{matrix}\right.\) \(\forall x\) \(\Rightarrow\) pt vô nghiệm
b/ Mình làm câu b, câu c bạn tự làm tương tự, 3 câu này cùng dạng
Lấy ln hai vế:
\(ln\left(3^{x^2-2}.4^{\dfrac{2x-3}{x}}\right)=ln18\Leftrightarrow ln3^{x^2-2}+ln4^{\dfrac{2x-3}{x}}-ln18=0\)
\(\Leftrightarrow\left(x^2-2\right)ln3+\dfrac{2x-3}{x}2ln2-ln\left(2.3^2\right)=0\)
\(\Leftrightarrow x^3ln3-2x.ln3+4x.ln2-6ln2-x.ln2-2x.ln3=0\)
\(\Leftrightarrow x^3ln3-4x.ln3+3x.ln2-6ln2=0\)
\(\Leftrightarrow x.ln3\left(x^2-4\right)+3ln2\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2ln3+2x.ln3+3ln2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-2=0\Rightarrow x=2\\x^2ln3+2x.ln3+3ln2=0\left(1\right)\end{matrix}\right.\)
Xét (1): \(\left(x^2+2x\right)ln3=-3ln2\Leftrightarrow x^2+2x=\dfrac{-3ln2}{ln3}=-3log_32\)
\(\Leftrightarrow\left(x+1\right)^2=1-3log_32=log_33-log_38=log_3\dfrac{3}{8}< 0\)
\(\Rightarrow\left(1\right)\) vô nghiệm
\(\Rightarrow\) pt có nghiệm duy nhất \(x=2\)
2/ Pt đã cho tương đương:
\(2017^{sin^2x}-2017^{cos^2x}=cos^2x-sin^2x\)
\(\Leftrightarrow2017^{sin^2x}+sin^2x=2017^{cos^2x}+cos^2x\)
Xét hàm \(f\left(t\right)=2017^t+t\) (\(0\le t\le1\))
\(\Rightarrow f'\left(t\right)=2017^t.ln2017+1>0\) \(\forall t\) \(\Rightarrow f\left(t\right)\) đồng biến
\(\Rightarrow f\left(t_1\right)=f\left(t_2\right)\Leftrightarrow t_1=t_2\)
\(\Rightarrow sin^2x=cos^2x\Rightarrow cos^2x-sin^2x=0\Rightarrow cos2x=0\)
\(\Rightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Thế k=0; k=1 ta được 2 nghiệm thuộc đoạn đã cho là \(x=\dfrac{\pi}{4};x=\dfrac{3\pi}{4}\)
\(\Rightarrow\) tổng nghiệm là \(T=\dfrac{\pi}{4}+\dfrac{3\pi}{4}=\pi\)

ĐKXĐ: \(6-5^x>0\Rightarrow5^x< 6\)
\(log_5\left(6-5^x\right)=1-x\Leftrightarrow6-5^x=5^{1-x}\)
\(\Leftrightarrow5^x-6+\frac{5}{5^x}=0\Leftrightarrow\left(5^x\right)^2-6.5^x+5=0\)
\(\Rightarrow\left[{}\begin{matrix}5^x=1\\5^x=5\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\) \(\Rightarrow\sum x=0+1=1\)

Ta xét các trường hợp sau:
+ TH1. x- 3= 1 hay x= 4. Khi đó; phương trình đã cho trở thành : 112= 1 luôn đúng.
=> x= 4 là nghiệm của phương trình.
+ TH2. .
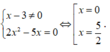
Vậy phương trình đã cho có ba nghiệm
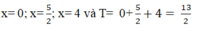
Chọn C.

Câu 1:
\(\Leftrightarrow x^2-4x+5+\sqrt{x^2-4x+5}-5=m\)
Đặt \(\sqrt{x^2-4x+5}=\sqrt{\left(x-2\right)^2+1}=a\ge1\)
\(\Rightarrow a^2+a-5=m\) (1)
Xét phương trình: \(x^2-4x+5=a^2\Leftrightarrow x^2-4x+5-a^2=0\)
\(\left\{{}\begin{matrix}x_1+x_2=4\\x_1x_2=5-a^2\end{matrix}\right.\)
\(\Rightarrow\) Nếu \(5-a^2>0\Rightarrow1\le a< \sqrt{5}\) thì pt có 2 nghiệm dương
Nếu \(5-a^2\le0\) \(\Leftrightarrow a\ge\sqrt{5}\) thì pt có 1 nghiệm dương
Vậy để pt đã cho có đúng 2 nghiệm dương thì: (1) có đúng 1 nghiệm thỏa mãn \(1\le a< \sqrt{5}\) hoặc có 2 nghiệm pb \(a_1>a_2\ge\sqrt{5}\)
Xét \(f\left(a\right)=a^2+a-5\) với \(a\ge1\)
\(f'\left(a\right)=0\Rightarrow a=-\frac{1}{2}< 1\Rightarrow f\left(a\right)\) đồng biến \(\forall a\ge1\) \(\Rightarrow y=m\) chỉ có thể cắt \(y=f\left(a\right)\) tại nhiều nhất 1 điểm có hoành độ \(a\ge1\)
\(f\left(1\right)=-3\) ; \(f\left(\sqrt{5}\right)=\sqrt{5}\)
\(\Rightarrow\) Để pt có 2 nghiệm pb đều dương thì \(-3\le m< \sqrt{5}\)
Câu 2:
\(x^2-3x+2\le0\Leftrightarrow1\le x\le2\) (1)
Ta có: \(mx^2+\left(m+1\right)x+m+1\ge0\)
\(\Leftrightarrow m\left(x^2+x+1\right)\ge-x-1\)
\(\Leftrightarrow m\ge\frac{-x-1}{x^2+x+1}=f\left(x\right)\) (2)
Để mọi nghiệm của (1) là nghiệm của (2) \(\Leftrightarrow\left(2\right)\) đúng với mọi \(x\in\left[1;2\right]\)
\(\Rightarrow m\ge\max\limits_{\left[1;2\right]}f\left(x\right)\)
\(f'\left(x\right)=\frac{-\left(x^2+x+1\right)+\left(2x+1\right)\left(x+1\right)}{\left(x^2+x+1\right)^2}=\frac{x^2+2x}{\left(x^2+x+1\right)^2}>0\) \(\forall x\in\left[1;2\right]\)
\(\Rightarrow f\left(x\right)\) đồng biến \(\Rightarrow\max\limits_{\left[1;2\right]}f\left(x\right)=f\left(2\right)=-\frac{3}{7}\)
\(\Rightarrow m\ge-\frac{3}{7}\)


ĐKXĐ: \(x>-1\)
Bước quan trọng nhất là tách hàm
\(\Leftrightarrow log_2\sqrt{x+3}-2\sqrt{x+3}+\left(x+3\right)=log_2\left(x+1\right)-2\left(x+1\right)+\left(x+1\right)^2\)
Đến đây coi như xong \(\Rightarrow\sqrt{x+3}=x+1\Rightarrow x=1\)