
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(N=lg\left(\tan1^0\right)+lg\left(\tan2^0\right)+....+lg\left(\tan88^0\right)+lg\left(\tan89^0\right)\)
\(=\left[lg\left(\tan1^0\right)+lg\left(\tan89^0\right)\right]+\left[lg\left(\tan2^0\right)+lg\left(\tan88^0\right)\right]+...+\left[lg\left(\tan44^0\right)+lg\left(\tan46^0\right)\right]+lg\left(\tan45^0\right)\)
\(=lg\left(\tan1^0.\tan89^0\right)+lg\left(\tan2^0.\tan88^0\right)+...+lg\left(\tan44^0.\tan46^0\right)+lg\left(\tan45^0\right)\)
\(=lg\left(\tan1^0.\cot1^0\right)+lg\left(\tan2^0.\cot2^0\right)+.....+lg\left(\tan44^0.\cot44^0\right)+lg\left(\tan45^0\right)\)
\(=lg1+lg1+....+lg1+lg1=0+0+....+0+0=0\)

a) Sử dụng công thức \(\frac{1}{\log_ba}=\log_ab\), hơn nữa \(x=2007!\) nên ta có : \(A=\log_x2+\log_x3+..........\log_x2007\)
\(=\log_x\left(2.3...2007\right)\)
\(=\log_xx=1\)
b) Nhận thấy
\(lg\tan1^o+lg\tan89^o=lg\left(lg\tan1^o.lg\tan89^o\right)=lg1=0\)
Tương tự ta có :
\(lg\tan2^o+lg\tan88^o=0\)
.................
\(lg\tan44^o+lg\tan46^o=0\)
\(lg\tan45^o=lg1=0\)
Do đó :
\(B=\left(lg\tan1^o+lg\tan89^o\right)+\left(lg\tan2^o+lg\tan88^o\right)+......+lg\tan45^0=0\)

Đặt \(t=lgx\), viết lại phương trình ở dạng :
\(3^2+3t.3-\left(t^4+t^3-2t^2\right)=0\)
Coi 3=u là ẩn, giải phương trình bậc 2 theo ẩn u,
\(\Delta=\left(2t^2+t\right)^2\)
tìm được
\(\begin{cases}u=-t^2-2t\\u=t^2-t\end{cases}\) và \(\begin{cases}x=10^{\frac{1+\sqrt{13}}{2}}\\x=10^{\frac{1-\sqrt{13}}{2}}\end{cases}\)

Đề như vậy hả bạn?
\(log^2x-logx.log_2\left(4x\right)+2log_2x=0\)
\(\Leftrightarrow log^2x-logx.\left(log_24+log_2x\right)+2log_2x=0\)
\(\Leftrightarrow log^2x-logx.\left(2+log_2x\right)+2log_2x=0\)
\(\Leftrightarrow log^2x-2logx-logx.log_2x+2log_2x=0\)
\(\Leftrightarrow logx\left(logx-2\right)-log_2x\left(logx-2\right)=0\)
\(\Leftrightarrow\left(logx-2\right)\left(logx-log_2x\right)=0\) \(\Rightarrow\left[{}\begin{matrix}logx=2\Rightarrow x=100\\logx-log_2x=0\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow logx-\dfrac{logx}{log2}=0\Rightarrow logx\left(1-\dfrac{1}{log2}\right)=0\Rightarrow logx=0\Rightarrow x=1\)
Vậy tổng các nghiệm là \(100+1=101\)

Chọn D.

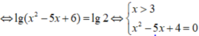
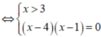
<=> x = 4
Vậy phương trình đã cho có nghiệm duy nhất là x= 4
Nhận xét : \(lg\tan1^0+lg\tan89^0=lg\left(\tan1^0.\tan89^0\right)=lg1=0\)
\(lg\tan2^0+lg\tan88^0=lg\left(\tan1^0.\tan88^0\right)=lg1=0\)
...................................................................................
....................................................................................
Và \(lg\tan45^0=lg1=0\)
Suy ra \(S=lg\tan1^0+lg\tan2^0+lg\tan3^0+......+lg\tan89^0\)
\(=\left(lg\tan1^0+lg\tan89^0\right)+\left(lg\tan2^0+lg\tan88^0\right)+....+lg\tan45^0\)
Vậy \(S=lg\tan1^0+lg\tan2^0+lg\tan3^0+...+lg\tan89^0=0\)