Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 14:
Vecto chỉ phương của đường thẳng $d$ là: $\overrightarrow{u_d}=(1; -1; 2)$
Mp $(P)$ vuông góc với $d$ nên nhận $\overrightarrow{u_d}$ là vecto pháp tuyến
Do đó PTMP $(P)$ là:
$1(x-x_M)-1(y-y_M)+2(z-z_M)=0$
$\Leftrightarrow x-y+2z=0$
Đáp án A
Bài 13:
Khi quay tam giác đều ABC quanh cạnh AB thì ta thu được một khối hình là hợp của 2 hình nón (ngược chiều nhau) có cùng bán kính đáy $r$ là đường cao của tam giác đều, tức là $r=\frac{\sqrt{3}}{2}.1=\frac{\sqrt{3}}{2}$ và đường cao là $h=\frac{AB}{2}=\frac{1}{2}$
Thể tích 1 hình nón: $V_n=\frac{1}{3}\pi r^2h=\frac{\pi}{8}$
Do đó thể tích của khối hình khi quay tam giác đều ABC quanh AB là: $2V_n=\frac{\pi}{4}$

15.
ĐKXĐ: \(x^2+2x+1>0\Rightarrow x\ne-1\)
\(\Leftrightarrow log_2\left(x^2+2x+1\right)>log_22\)
\(\Leftrightarrow x^2+2x+1>2\)
\(\Leftrightarrow x^2+2x-1>0\Rightarrow\left[{}\begin{matrix}x< -1-\sqrt{2}\\x>-1+\sqrt{2}\end{matrix}\right.\)
16.
\(J=4\int\limits^2_0f\left(x\right)dx-\int\limits^2_02xdx=4.3-x^2|^2_0=8\)
17.
\(z=2+2i-6i-6i^2=8-4i\)
\(\Rightarrow\overline{z}=8+4i\)
11.
\(S=4\pi R^2\Rightarrow R=\sqrt{\frac{S}{4\pi}}=2\left(cm\right)\)
12.
\(log\left(10a^3\right)=log10+loga^3=1+3loga\)
13.
\(S=\pi R^2\Rightarrow R=\sqrt{\frac{S}{\pi}}\)
\(\Rightarrow S_{xq}=2\pi R.l=2\pi\sqrt{\frac{S}{\pi}}.l=2l.\sqrt{\pi S}\)
14.
\(\lim\limits_{x\rightarrow-1}\frac{x-2}{x+1}=-\infty\Rightarrow x=-1\) là tiệm cận đứng

14.
\(log_aa^2b^4=log_aa^2+log_ab^4=2+4log_ab=2+4p\)
15.
\(\frac{1}{2}log_ab+\frac{1}{2}log_ba=1\)
\(\Leftrightarrow log_ab+\frac{1}{log_ab}=2\)
\(\Leftrightarrow log_a^2b-2log_ab+1=0\)
\(\Leftrightarrow\left(log_ab-1\right)^2=0\)
\(\Rightarrow log_ab=1\Rightarrow a=b\)
16.
\(2^a=3\Rightarrow log_32^a=1\Rightarrow log_32=\frac{1}{a}\)
\(log_3\sqrt[3]{16}=log_32^{\frac{4}{3}}=\frac{4}{3}log_32=\frac{4}{3a}\)
11.
\(\Leftrightarrow1>\left(2+\sqrt{3}\right)^x\left(2+\sqrt{3}\right)^{x+2}\)
\(\Leftrightarrow\left(2+\sqrt{3}\right)^{2x+2}< 1\)
\(\Leftrightarrow2x+2< 0\Rightarrow x< -1\)
\(\Rightarrow\) có \(-2+2020+1=2019\) nghiệm
12.
\(\Leftrightarrow\left\{{}\begin{matrix}x-2>0\\0< log_3\left(x-2\right)< 1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>2\\1< x-2< 3\end{matrix}\right.\)
\(\Rightarrow3< x< 5\Rightarrow b-a=2\)
13.
\(4^x=t>0\Rightarrow t^2-5t+4\ge0\)
\(\Rightarrow\left[{}\begin{matrix}t\le1\\t\ge4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}4^x\le1\\4^x\ge4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x\le0\\x\ge1\end{matrix}\right.\)

8.
\(a^2+9b^2=10ab\Leftrightarrow a^2+6ab+9b^2=16ab\)
\(\Leftrightarrow\left(a+3b\right)^2=16ab\)
\(\Rightarrow log\left(a+3b\right)^2=log\left(16ab\right)\)
\(\Rightarrow2log\left(a+3b\right)=log16+loga+logb\)
\(\Leftrightarrow log\left(a+3b\right)-\frac{log4^2}{2}=\frac{loga+logb}{2}\)
\(\Leftrightarrow log\left(a+3b\right)-log4=\frac{loga+logb}{2}\)
\(\Leftrightarrow log\frac{a+3b}{4}=\frac{loga+logb}{2}\)
9.
Tung độ của điểm M bằng 0 nên nó nằm trên mặt phẳng Oxz
5.
\(z^2+4z+5=0\Leftrightarrow\left(z+2\right)^2=-1=i^2\)
\(\Rightarrow\left[{}\begin{matrix}z+2=i\\z+2=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}z_2=-2+i\\z_1=-2-i\end{matrix}\right.\)
\(\Rightarrow w=z_1-2z_2=2-3i\)
\(\Rightarrow\left|w\right|=\sqrt{2^2+\left(-3\right)^2}=\sqrt{13}\)
6.
\(\overrightarrow{AB}=\left(1;2;1\right)\Rightarrow\) mặt phẳng (P) nhận (1;2;1) là 1 vtpt
Pt (P): \(1\left(x-0\right)+2\left(y-1\right)+1\left(z-1\right)=0\)
\(\Leftrightarrow x+2y+z-3=0\)
7.
Đề chắc ghi sai, có phải đề đúng là xác suất để ko có học sinh nam nào ngồi cạnh nhau?
Xếp bất kì: có \(9!\) cách
Xếp 6 bạn nữ có \(6!\) cách, 6 bạn nữ này tạo ra 7 vị trí trống, xếp 3 bạn nam vào các vị trí trống đó có \(A_7^3\) cách
Xác suất: \(P=\frac{6!.A_7^3}{9!}=\frac{5}{12}\)

11.
Thay tọa độ M vào pt d ta được:
\(\frac{1}{1}=\frac{3}{3}=\frac{m}{-2}\Rightarrow m=-2.1=-2\)
12.
\(AA'\perp\left(ABC\right)\Rightarrow AB\) là hình chiếu vuông góc của A'B lên (ABC)
\(\Rightarrow\widehat{A'BA}\) là góc giữa A'B và (ABC)
\(\Rightarrow\widehat{A'BA}=60^0\)
\(AB=\frac{AC}{\sqrt{2}}=2a\Rightarrow AA'=AB.tan60^0=2a\sqrt{3}\)
8.
\(I=2\int\limits^9_0f\left(x\right)dx+3\int\limits^9_0g\left(x\right)dx=2.37+3.???=...\)
Đề thiếu, bạn tự điền số và tính
9.
\(z=\frac{1}{3-4i}=\frac{3+4i}{\left(3-4i\right)\left(3+4i\right)}=\frac{3}{25}+\frac{4}{25}i\)
\(\Rightarrow\overline{z}=\frac{3}{25}-\frac{4}{25}i\)
10.
\(\overline{z_1}=1-5i\) \(\Rightarrow\overline{z_1}+iz_2=1-5i+i\left(3-2i\right)=3-2i\)
Điểm biểu diễn là \(Q\left(3;-2\right)\)

14.
Mặt phẳng (P) nhận \(\overrightarrow{n}=\left(2;1;-2\right)\) là 1 vtpt
Đường thẳng d nhận \(\overrightarrow{u}=\left(1;-2;3\right)\) là 1 vtcp
Điểm \(M\left(2;0;-3\right)\) thuộc d nên cũng thuộc (Q)
(Q) vuông góc (P) và chứa d nên nhận \(\left[\overrightarrow{n};\overrightarrow{u}\right]=\left(1;8;5\right)\) là 1 vtpt
Phương trình (Q):
\(1\left(x-2\right)+8y+5\left(z+3\right)=0\)
\(\Leftrightarrow x+8y+5z+13=0\)
15.
Phương trình hoành độ giao điểm:
\(sinx=cosx\Rightarrow x=\frac{\pi}{4}\)
\(S=\int\limits^{\frac{\pi}{4}}_0\left(cosx-sinx\right)dx+\int\limits^{\pi}_{\frac{\pi}{4}}\left(sinx-cosx\right)dx=\sqrt{2}-1+\sqrt{2}+1=2\sqrt{2}\)
10.
Coi lại đề nào bạn, pt hình phẳng (D) có vấn đề, nhìn chữ -dx+4 kia ko biết phải nghĩ sao
11.
Cũng ko dịch được đề này, đoán đại: cho \(F\left(x\right)=x^2\) là 1 nguyên hàm của \(f\left(x\right).e^{2x}\). Tìm nguyên hàm của \(f'\left(x\right).e^{2x}\)
\(I=\int f'\left(x\right)e^{2x}dx\)
Đặt \(\left\{{}\begin{matrix}u=e^{2x}\\dv=f'\left(x\right)dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2e^{2x}dx\\v=f\left(x\right)\end{matrix}\right.\)
\(\Rightarrow I=e^{2x}f\left(x\right)-2\int f\left(x\right)e^{2x}dx=e^{2x}f\left(x\right)-2x^2+C\)
12.
Đúng là \(y=\left(e+1\right)x\) và \(y=1+e^x\) chứ bạn? Hai đồ thị này cắt nhau tại 2 điểm, nhưng ko thể tìm được tọa độ của điểm thứ 2 đâu
13.
Hình chiếu của A lên Ox có tọa độ \(\left(1;0;0\right)\)

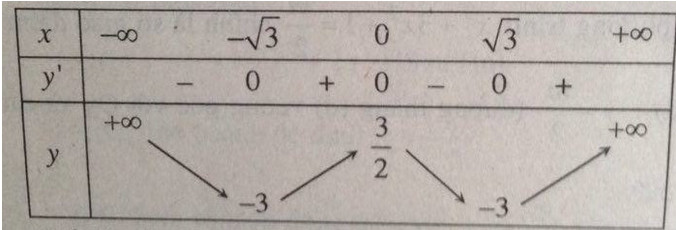
a) Xét hàm số y = f(x)=12x4−3x2+32f(x)=12x4−3x2+32 (C) có tập xác định: D = R
y’ = 2x3 – 6x = 2x(x2 – 3)
y’ = 0 ⇔ x = 0, x = ±√3
Bảng biến thiên:
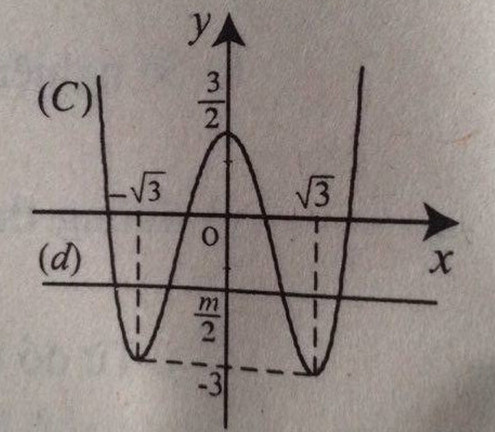
Đồ thị hàm số:
b)
y’’ = 6x2 – 6x
y’’ = 0 ⇔ 6x2 – 6x = 0 ⇔ x = ± 1
y’(-1) = 4, y’’(1) = -4, y(± 1) = -1
Tiếp tuyến của (C) tại điểm (-1, -1) là : y = 4(x+1) – 1= 4x+3
Tiếp tuyến của (C) tại điểm (1, -1) là: y = -4(x-1) – 1 = -4x + 3
c) Ta có: \(x^4-6x^2+3=m\)\(\Leftrightarrow\dfrac{x^4}{2}-3x^2+\dfrac{3}{2}=\dfrac{m}{2}\).
Số nghiệm của (1) là số giao điểm của (C) và đường thẳng (d) : \(y=\dfrac{m}{2}\).
Dễ thấy:
m < -6: ( 1) vô nghiệm
m = -6 : (1) có 2 nghiệm
-6 < m < 3: (1) có 4 nghiệm
m = 3: ( 1) có 3 nghiệm
m > 3: (1) có 2 nghiệm
Đáp án : B.