Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : P = \(\dfrac{1}{1975}\left(\dfrac{2}{1945}-1\right)-\dfrac{1}{1945}\left(1-\dfrac{2}{1975}\right)+\dfrac{1974}{1975}.\dfrac{1946}{1945}\)
\(-\dfrac{3}{1975.1945}\)
= \(\dfrac{2}{1975.1945}-\dfrac{1}{1975}-\dfrac{1}{1945}+\dfrac{2}{1975.1945}+\dfrac{1974}{1975}.\dfrac{1946}{1945}\)
\(-\dfrac{3}{1975.1945}\)
= \(\dfrac{2+2+1974.1946-3-1975-1945}{1975.1945}\)
= \(\dfrac{2+2+1974.1946-3-1975-1945}{1975.1945}\)
= \(\dfrac{1973}{1975}\)

\(\begin{array}{l}a)\dfrac{{{x^2} - 49}}{{{x^2} + 5}}.\left( {\dfrac{{{x^2} + 5}}{{x - 7}} - \dfrac{{{x^2} + 5}}{{x + 7}}} \right)\\ = \dfrac{{\left( {x - 7} \right)\left( {x + 7} \right)}}{{{x^2} + 5}}.\dfrac{{{x^2} + 5}}{{x - 7}} - \dfrac{{\left( {x - 7} \right)\left( {x + 7} \right)}}{{{x^2} + 5}}.\dfrac{{{x^2} + 5}}{{x + 7}}\\ = x + 7 - \left( {x - 7} \right) = 14\end{array}\)
\(\begin{array}{l}b)\dfrac{{19{\rm{x}} + 8}}{{x + 1975}}.\dfrac{{2000 - x}}{{x + 1945}} + \dfrac{{19{\rm{x}} + 8}}{{x + 1975}}.\dfrac{{2{\rm{x}} - 25}}{{x + 1945}}\\ = \dfrac{{19{\rm{x}} + 8}}{{x + 1975}}.\left( {\dfrac{{2000 - x}}{{x + 1945}} + \dfrac{{2{\rm{x}} - 25}}{{x + 1945}}} \right)\\ = \dfrac{{19{\rm{x}} + 8}}{{x + 1975}}.\dfrac{{2000 - x + 2{\rm{x}} - 25}}{{x + 1945}}\\ = \dfrac{{19{\rm{x}} + 8}}{{x + 1975}}.\dfrac{{x + 1975}}{{x + 1945}} = \dfrac{{19{\rm{x}} + 8}}{{x + 1945}}\end{array}\)

b: Đặt \(x^2-6x-2=a\)
Theo đề, ta có: \(a+\dfrac{14}{a+9}=0\)
=>(a+2)(a+7)=0
\(\Leftrightarrow\left(x^2-6x\right)\left(x^2-6x+5\right)=0\)
=>x(x-6)(x-1)(x-5)=0
hay \(x\in\left\{0;1;6;5\right\}\)
c: \(\Leftrightarrow\dfrac{-8x^2}{3\left(2x-1\right)\left(2x+1\right)}=\dfrac{2x}{3\left(2x-1\right)}-\dfrac{8x+1}{4\left(2x+1\right)}\)
\(\Leftrightarrow-32x^2=8x\left(2x+1\right)-3\left(8x+1\right)\left(2x-1\right)\)
\(\Leftrightarrow-32x^2=16x^2+8x-3\left(16x^2-8x+2x-1\right)\)
\(\Leftrightarrow-48x^2=8x-48x^2+18x+3\)
=>26x=-3
hay x=-3/26

a: Ta có: \(4x-2\left(1-x\right)=5\left(x-4\right)\)
\(\Leftrightarrow4x-2+2x=5x-20\)
\(\Leftrightarrow x=-18\)
b: Ta có: \(\dfrac{x}{6}+\dfrac{1-3x}{9}=\dfrac{-x+1}{12}\)
\(\Leftrightarrow6x+4\left(1-3x\right)=3\left(-x+1\right)\)
\(\Leftrightarrow6x+4-12x=-3x+3\)
\(\Leftrightarrow-3x=-1\)
hay \(x=\dfrac{1}{3}\)
c: Ta có: \(\left(x+2\right)^2-3\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)
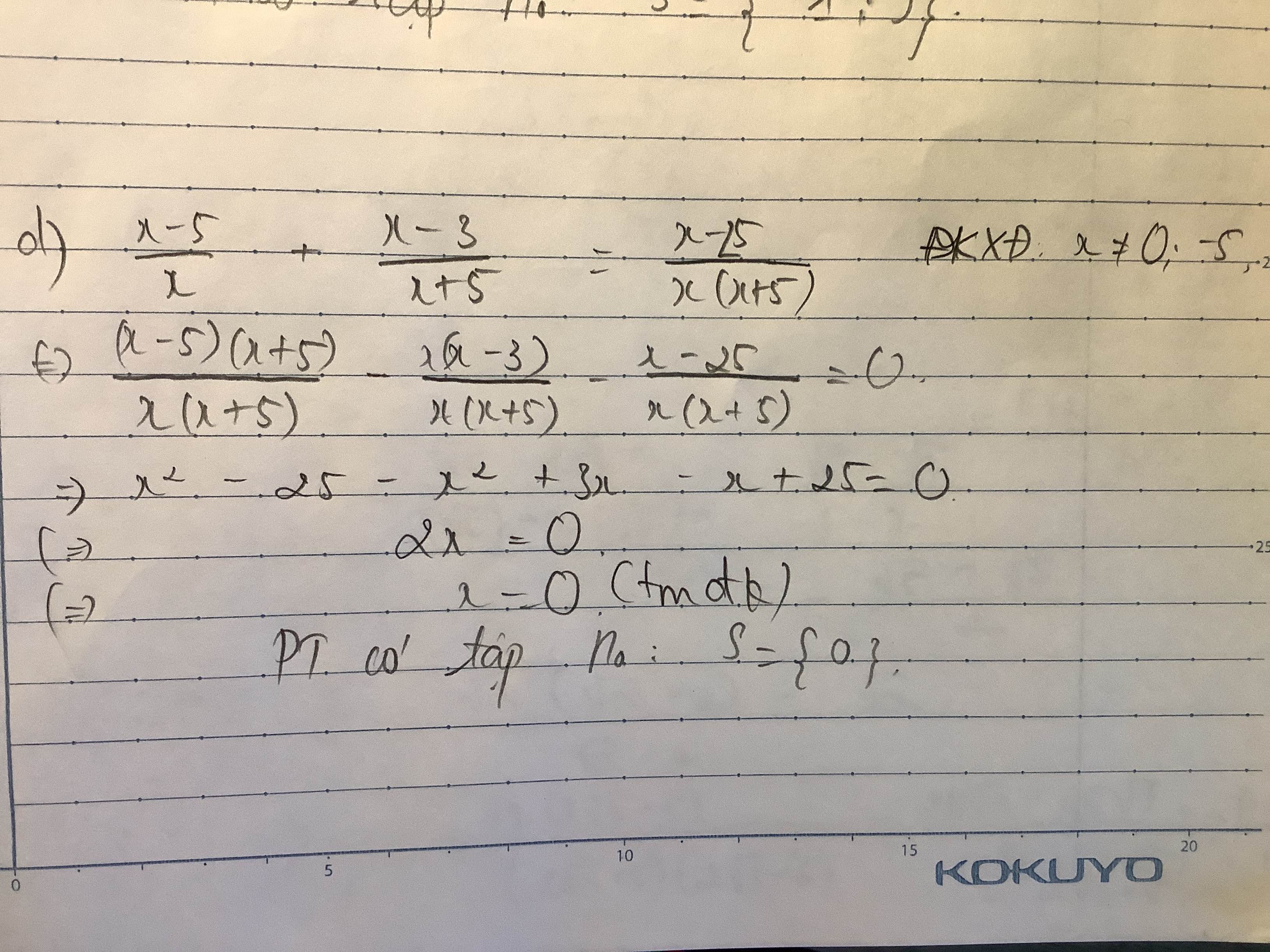
a) \(A=85^2-45^2+75^2-35^2+65^2-25^2+55^2-15^2\)
\(A=\left(85-45\right)\left(85+45\right)+....+\left(55-15\right)\left(55+15\right)\)
\(A=40.130+40.110+40.90+40.70\)
\(A=40.\left(130+110+90+70\right)=40.400=16000\)
b) \(B=\left(1-2\right)\left(1+2\right)+\left(3-4\right)\left(3+4\right)+...+\left(2011-2012\right)\left(2011+2012\right)\)
\(B=-3-7-11-...-4023\)
\(B=-\left(3+7+11+...+4023\right)\)
\(B=-\dfrac{\left(3+4023\right)\left[\dfrac{\left(4023-3\right)}{4}+1\right]}{2}=2025078\)