Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(C=180^0-\left(A+B\right)=75^0\)
Áp dụng định lý hàm sin:
\(\dfrac{b}{sinB}=\dfrac{c}{sinC}\Rightarrow c=\dfrac{b.sinC}{sinB}=\dfrac{8.sin75^0}{sin45^0}=4+4\sqrt{3}\)

Bài 2:
\(E=\left(\dfrac{1}{2}+1\right)\left(\dfrac{1}{3}+1\right)\left(\dfrac{1}{4}+1\right)...\left(\dfrac{1}{99}+1\right)\)
\(\Leftrightarrow E=\dfrac{3}{2}.\dfrac{4}{3}.\dfrac{5}{4}...\dfrac{100}{99}\)
\(\Leftrightarrow E=\dfrac{3.4.5...100}{2.3.4...99}\)
\(\Leftrightarrow E=\dfrac{\left(3.4.5...99\right).100}{2.\left(3.4...99\right)}\)
\(\Leftrightarrow E=\dfrac{100}{2}=50\)
Vậy ...

Bài 1:
a) \(S=1+2+3+4+5+6+7+8+9\)
\(=\left(1+9\right)+\left(2+8\right)+\left(3+7\right)+\left(4+6\right)+5\)
\(=10+10+10+10+5\)
\(=45\)
b) lm như bài này: Câu hỏi của Thái Minh Tuệ - Toán lớp 4 - Học toán với OnlineMath
S=(1+9)+(2+8)+(3+7)+(4+6)+5=10+10+10+10+5![]()
M=so so hang cua tong M la
(101-1):1+1=101
tong cua M la
(101+1):2x101=5151

Câu 1:
Chú ý độ dài 3 cạnh của tam giác là sai thì \(a+b=7=c\)
Nếu là cạnh của tam giác thì: \(\left\{{}\begin{matrix}a+b>c\\a+c>b\\c+b>a\end{matrix}\right.\)
Câu 2: Ta có:
\(m_a=\sqrt{\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}}=\sqrt{\dfrac{AC^2+AB^2}{2}-\dfrac{BC^2}{4}}\)
\(\Rightarrow m_a=\sqrt{\dfrac{9^2+4^2}{2}-\dfrac{6^2}{4}}\)
\(\Rightarrow m_a\approx6,3\)
Ta có: \(p=\dfrac{AB+AC+BC}{2}=\dfrac{4+6+9}{2}=\dfrac{19}{2}\)
\(\Rightarrow S_{ABC}=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=\sqrt{\dfrac{19}{2}\cdot\left(\dfrac{19}{2}-6\right)\cdot\left(\dfrac{19}{2}-9\right)\cdot\left(\dfrac{19}{2}-4\right)}\approx9,5\)
\(\Rightarrow h_b=2\cdot\dfrac{S_{ABC}}{b}\Rightarrow h_b=2\cdot\dfrac{9,5}{9}\approx2,1\)

B={x\(\in\)N|x=3k; 1<=k<=4}
C={x\(\in\)N|x=4*a2; 1<=a<=5}
D={x\(\in\)N|x=9*a2;1<=a<=4}
E={x\(\in\)N|x=4k; 0<=x<=4}
G={x\(\in\)N|x=(-3)^k; 1<=k<=4}

a: \(=\dfrac{54-34}{189-119}=\dfrac{20}{70}=\dfrac{2}{7}\)
b: \(=\dfrac{6+6\cdot4+6\cdot49}{15+15\cdot4+15\cdot49}=\dfrac{6}{15}=\dfrac{2}{5}\)
c: \(=\dfrac{13\left(3-18\right)}{40\left(15-2\right)}=\dfrac{-15}{40}=-\dfrac{3}{8}\)

a) \(A=2+6+8+10+....+2018\)
\(A=2\left(1+2+3+4+....+1009\right)\)
ta có \(1+2+3+4+...+n=\dfrac{\left(n+1\right).n}{2}\)
với n=1009 ta có \(1+2+3+....+1009=\dfrac{1010.1009}{2}\)
\(\Rightarrow A=2.\dfrac{1010.1009}{2}=1010.1009\)
\(B=2018-2017+2016-2015+....+2-1\)
\(B=1+1+1+1+....+1\)
tất cả có 2018 số mà cứ hiệu 2 số =1 vậy B có 1009 số 1
vậy \(B=1009\)
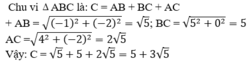
a/ \(19.64+76.34\)
\(=19.4.16+19.4.34\)
\(=19.4\left(16+34\right)\)
\(19.4.50\)
\(=19.200=3800\)
b, \(136.68+16.272\)
\(=136.68+32.136\)
\(=136\left(68+32\right)\)
\(=136.100=13600\)
c/ \(\left(2+4+6+..........+100\right)\left(36.3.333-108.111\right)\)
\(=\left(2+4+....+100\right)\left(36.3.111-108.100\right)\)
\(=\left(2+4+.......+100\right)\left(108.111-108.111\right)\)
\(\left(2+4+...+100\right).0=0\)
bạn làm đúng rồi