Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có A B → = 2 ; − 2 B C → = 2 ; 2 C A → = − 4 ; 0 ⇒ A B = 2 2 + − 2 2 = 2 2 B C = 2 2 + 2 2 = 2 2 C A = − 4 2 + 0 2 = 4
Vậy chu vi P của tam giác ABC là P =AB + BC + CA = 4 + 4 2
Chọn B.

a: vecto AB=(1;1)
vecto AC=(2;6)
vecto BC=(1;5)
b: \(AB=\sqrt{1^2+1^2}=\sqrt{2}\)
\(AC=\sqrt{2^2+6^2}=2\sqrt{10}\)
\(BC=\sqrt{1^2+5^2}=\sqrt{26}\)
=>\(C=\sqrt{2}+2\sqrt{10}+\sqrt{26}\)
c: Tọa độ trung điểm của AB là:
x=(1+2)/2=1,5 và y=(-1+0)/2=-0,5
Tọa độ trung điểm của AC là;
x=(1+3)/2=2 và y=(-1+5)/2=4/2=2
Tọa độ trung điểm của BC là:
x=(2+3)/2=2,5 và y=(0+5)/2=2,5
d: ABCD là hình bình hành
=>vecto AB=vecto DC
=>3-x=1 và 5-y=1
=>x=2 và y=4

Đáp án B
Thay tọa độ điểm A vào phương trình đường thẳng d ta được -2.
Thay tọa độ điểm B vào phương trình đường thẳng d ta được -10.
Thay tọa độ điểm C vào phương trình đường thẳng d ta được. -11.
Suy ra:
A và B; B và C; C và A đôi một nằm cùng phía đối với d. Nên đường thẳng d không cắt cạnh nào của tam giác.

\(AB=\sqrt{\left(5-1\right)^2+\left(-3+1\right)^2}=2\sqrt{5}\)
\(AC=\sqrt{\left(0-1\right)^2+\left(1+1\right)^2}=\sqrt{5}\)
\(BC=\sqrt{\left(0-5\right)^2+\left(1+3\right)^2}=\sqrt{29}\)
=>C=3 căn 5+căn 29

Giả sử tâm đường tròn là điểm \(I\left( {a;b} \right)\). Ta có: \(IA = IB = IC \Leftrightarrow I{A^2} = I{B^2} = I{C^2}\)
Vì \(I{A^2} = I{B^2},I{B^2} = I{C^2}\) nên: \(\left\{ \begin{array}{l}{\left( {6 - a} \right)^2} + {\left( { - 2 - b} \right)^2} = {\left( {4 - a} \right)^2} + {\left( {2 - b} \right)^2}\\{\left( {4 - a} \right)^2} + {\left( {2 - b} \right)^2} = {\left( {5 - a} \right)^2} + {\left( { - 5 - b} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 2\end{array} \right.\)
Vậy \(I\left( {1; - 2} \right)\) và \(R = IA = \sqrt {{{\left( {1 - 6} \right)}^2} + {{\left( { - 2 + 2} \right)}^2}} = 5\)
Vậy phương trình đường tròn đi qua 3 điểm A,B, C là: \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 25\)
Cách 2:
Gọi phương trình đường tròn cần tìm là (C):\({x^2} + {y^2} + 2ax + 2by + c = 0\) \(\left( {{a^2} + {b^2} - c > 0} \right)\)
\(A(6; -2), B(4; 2), C(5; -5)\) thuộc (C) nên ta có:
\(\left\{ {\begin{array}{*{20}{l}}
{36 + 4 + 12a - 4b + c = 0}\\
{16 + 4 + 8a + 4b + c = 0}\\
{25 + 25 + 10a - 10b + c = 0}
\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{12a - 4b + c = - 40}\\
{8a + 4b + c = - 20}\\
{10a - 10b + c = - 50}
\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a = - 1}\\
{b = 2} \,\rm{(thỏa mãn)}\\
{c = - 20}
\end{array}} \right.\)
Vậy phương trình đường tròn đi qua 3 điểm A, B, C là: \({x^2} + {y^2} - 2x + 4y -20 = 0\) hay \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 25\)

Đáp án A
A B = 5 − 2 2 + − 1 − 3 2 = 5 , A C = 7 − 2 2 + − 9 − 3 2 = 13
B C = 7 − 5 2 + − 9 + 1 2 = 2 17
Chu vi tam giác ABC là: 5 + 13 + 2 17 = 18 + 2 17
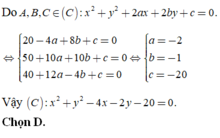
Chọn C.