
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

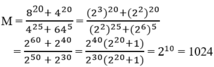

\(M=\frac{8^{20}+4^{20}}{4^{25}+64^5}\)
\(M=\frac{\left(2^3\right)^{20}+\left(2^2\right)^{20}}{\left(2^2\right)^{25}+\left(2^6\right)^5}\)
\(M=\frac{2^{60}+2^{40}}{2^{50}+2^{30}}\)
\(M=\frac{2^{40}\left(2^{20}+1\right)}{2^{30}\left(2^{20}+1\right)}\)
\(M=2^{10}\)
\(M=1024\)

\(\frac{8^{20}+4^{20}}{4^{25}+64^5}=\frac{\left(2^3\right)^{20}+\left(2^2\right)^{20}}{\left(2^2\right)^{25}+\left(2^6\right)^5}=\frac{2^{60}+2^{40}}{2^{50}+2^{30}}=\frac{2^{40}\times\left(2^{20}+1\right)}{2^{30}\times\left(2^{20}+1\right)}=2^{10}=1024\)
Chúc bạn học tốt ^^

\(M=\frac{\left(2^3\right)^{20}+\left(2^2\right)^{20}}{\left(2^2\right)^{25}+\left(2^6\right)^5}=\frac{2^{60}+2^{40}}{2^{50}+2^{30}}=\frac{2^{40}\left(2^{20}+1\right)}{2^{30}\left(2^{20}+1\right)}=2^{10}\)
\(M=\frac{8^{20}+4^{20}}{4^{25}+64^5}\)
= \(\frac{\left(2^3\right)^{20}+\left(2^2\right)^{20}}{\left(2^2\right)^{25}+\left(2^6\right)^5}=\frac{2^{60}+2^{40}}{2^{50}+2^{30}}=\frac{2^{40}\left(2^{20}+1\right)}{2^{30}\left(2^{20}+1\right)}=2^{10}\)

\(M=\frac{4^{20}.\left(2^{20}+1\right)}{4^{15}.\left(4^{10}+1\right)}\)
\(M=4^5\)
\(M=1024\)
Chúc bạn học tốt cho mik k nha.Thanks

\(M=\frac{8^{20}+4^{20}}{4^{25}+64^5}\)
\(=\frac{\left(2^3\right)^{20}+\left(2^2\right)^{20}}{\left(2^2\right)^{25}+\left(2^6\right)^5}\)
\(=\frac{2^{60}+2^{40}}{2^{50}+2^{30}}\)
\(=\frac{2^{40}\left(2^{20}+1\right)}{2^{30}\left(2^{20}+1\right)}\)
\(=\frac{2^{40}}{2^{30}}=2^{10}\)
\(\frac{8^{20}+4^{20}}{4^{25}+64^5}\)
\(=\frac{\left(2^3\right)^{20}+\left(2^2\right)^{20}}{\left(2^2\right)^{25}+\left(2^6\right)^5}\)
\(=\frac{2^{60}+2^{40}}{2^{25}+2^{30}}\)
\(=\frac{2^{40}\left(2^{20}+1\right)}{2^{25}\left(1+2^5\right)}\)
\(=\frac{2^{15}\left(2^{20}+1\right)}{1+2^5}\)
\(=\frac{2^{35}+2^{15}}{1+2^5}\)

\(M=\dfrac{8^{20}+4^{20}}{4^{25}+64^5}=\dfrac{\left(2^3\right)^{20}+\left(2^2\right)^{20}}{\left(2^2\right)^{25}+\left(2^6\right)^5}=\dfrac{2^{60}+2^{40}}{2^{50}+2^{30}}=\)
\(=\dfrac{2^{40}\left(2^{20}+1\right)}{2^{30}\left(2^{20}+1\right)}=2^{10}=1024\)
\(\dfrac{8^{20}+4^{20}}{4^{25}+64^5}=\dfrac{\left(2^3\right)^{20}+\left(2^2\right)^{20}}{\left(2^2\right)^{25}+\left(2^6\right)^5}=\dfrac{2^{60}+2^{40}}{2^{50}+2^{30}}=\dfrac{2^{40}\times\left(2^{20}+1\right)}{2^{30}\times\left(2^{20}+1\right)}=2^{10}=1024\)

\(M=\frac{\left(2^3\right)^{20}+\left(2^2\right)^{20}}{\left(2^2\right)+\left(2^6\right)^5}\)
\(M=\frac{2^{60}+2^{40}}{2^{50}+2^{30}}\)
\(M=\frac{2^{40}\cdot2^{20}+2^{40}\cdot1}{2^{30}\cdot2^{20}+2^{30}\cdot1}\)
\(M=\frac{2^{40}\cdot\left(2^{20}+1\right)}{2^{30}\cdot\left(2^{20}+1\right)}\)
\(M=\frac{2^{40}}{2^{30}}\)
\(M=2^{40-30}\)
\(M=2^{10}\)
\(M=1024\)

\(M=\frac{8^{20}+4^{20}}{4^{25}+64^5}=\frac{4^{20}.\left(2^{20}+1\right)}{4^{25}+\left(4^3\right)^5}=\frac{4^{20}.\left(2^{20}+1\right)}{4^{25}+4^{15}}\)
\(=\frac{4^{20}.\left(4^{10}+1\right)}{4^{25}.\left(4^{10}+1\right)}=\frac{1}{4^5}=\frac{1}{1024}\)

a: \(\dfrac{8^{20}+4^{20}}{4^{25}+64^5}=\dfrac{2^{60}+2^{40}}{2^{50}+2^{30}}=\dfrac{2^{40}\left(2^{20}+1\right)}{2^{30}\left(2^{20}+1\right)}=2^{10}\)
b: \(\dfrac{45^{10}\cdot5^{20}}{75^{15}}=\dfrac{5^{30}\cdot3^{20}}{3^{15}\cdot5^{30}}=3^5\)
a)\(\dfrac{8^{20}+4^{20}}{4^{25}+64^5}=\dfrac{2^{60}+2^{40}}{2^{50}+2^{30}}=\dfrac{2^{40}\left(2^{20}+1\right)}{2^{30}\left(2^{20}+1\right)}=2^{10}=1024\)
b)\(\dfrac{45^{10}\cdot5^{20}}{75^{15}}=\dfrac{9^{10}\cdot5^{30}}{3^{15}\cdot5^{30}}=\dfrac{3^{20}}{3^{15}}=3^5=243\)

\(\frac{8^{20}+4^{20}}{4^{25}+64^5}\)=\(\frac{\left(2^3\right)^{20}+\left(2^2\right)^{20}}{\left(2^2\right)^{25}+\left(2^6\right)^5}\)=\(\frac{2^{60}+2^{40}}{2^{50}+2^{30}}\)=\(\frac{2^{40}\left(2^{20}+1\right)}{2^{30}\left(2^{20}+1\right)}\)=\(\frac{2^{40}}{2^{30}}\)= 210