Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Lập bảng giá trị:
| x | -4 | -2 | 0 | 2 | 4 |
| y = -0,75x2 | -12 | -3 | 0 | -3 | -12 |
- Vẽ đồ thị:
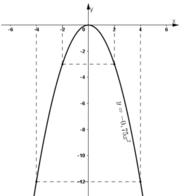
- Quan sát đồ thị hàm số y = -0,75x2:
Khi x tăng từ -2 đến 4, y tăng từ -3 đến 0 rồi lại giảm xuống -12.
Vậy: Giá trị nhỏ nhất của y = -12 đạt được khi x = 4
Giá trị lớn nhất của y = 0 đạt được khi x = 0.

- Lập bảng giá trị:
| x | -4 | -2 | 0 | 2 | 4 |
| y = - 0 , 75 x 2 | -12 | -3 | 0 | -3 | -12 |
- Vẽ đồ thị:
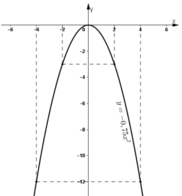
- Quan sát đồ thị hàm số y = - 0 , 75 x 2 :
Khi x tăng từ -2 đến 4, y tăng từ -3 đến 0 rồi lại giảm xuống -12.
Vậy: Giá trị nhỏ nhất của y = -12 đạt được khi x = 4
Giá trị lớn nhất của y = 0 đạt được khi x = 0.

\(x^2+y^2+xy=3\)
Có \(x^2+y^2\ge2xy\) \(\Rightarrow3=x^2+y^2+xy\ge2xy+xy\) \(\Leftrightarrow xy\le1\)
\(x^2+y^2\ge-2xy\) \(\Rightarrow3=x^2+y^2+xy\ge-2xy+xy\) \(\Leftrightarrow-3\le xy\)
Đặt A= \(x^2+y^2-xy=\left(3-xy\right)-xy=3-2xy\)
mà \(-3\le xy\le1\) \(\Rightarrow9\ge3-2xy\ge1\)
=> minA=1 <=> \(\left\{{}\begin{matrix}xy=1\\x=y\end{matrix}\right.\) <=>x=y=1
maxA=9 <=>\(\left\{{}\begin{matrix}xy=-3\\x=-y\end{matrix}\right.\) <=>\(\left(x;y\right)=\left(\sqrt{3};-\sqrt{3}\right);\left(-\sqrt{3};\sqrt{3}\right)\)
Đặt \(P=x^2+y^2-xy\)
\(\Rightarrow\dfrac{P}{3}=\dfrac{x^2+y^2-xy}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}\)
\(\dfrac{P}{3}=\dfrac{3x^2+3y^2-3xy}{3\left(x^2+y^2+xy\right)}=\dfrac{x^2+y^2+xy+2\left(x^2+y^2-2xy\right)}{3\left(x^2+y^2+xy\right)}\)
\(\dfrac{P}{3}=\dfrac{1}{3}+\dfrac{2\left(x-y\right)^2}{3\left(x^2+y^2+xy\right)}\ge\dfrac{1}{3}\Rightarrow P\ge1\)
\(P_{min}=1\) khi \(x=y=1\)
\(\dfrac{P}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}=\dfrac{3\left(x^2+y^2+xy\right)-2\left(x^2+y^2+2xy\right)}{x^2+y^2+xy}=3-\dfrac{2\left(x+y\right)^2}{x^2+y^2+xy}\le3\)
\(\Rightarrow P\le9\)
\(P_{max}=9\) khi \(\left(x;y\right)=\left(\sqrt{3};-\sqrt{3}\right);\left(-\sqrt{3};\sqrt{3}\right)\)

Lời giải:
$9< x^2< 99$. Mà $x$ nguyên nên $x^2$ là số chính phương.
$\Rightarrow x^2\in \left\{16; 25; 36; 49; 64; 81\right\}$
$\Rightarrow x_{\min}=-9; x_{\max}=9$
Hiệu giữa số $x$ lớn nhất và nhỏ nhất là: $9-(-9)=18$