Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(A=\dfrac{1}{2}.\dfrac{4}{3}.\dfrac{9}{8}.\dfrac{16}{15}...\dfrac{2016^2}{2015.2017}\)
\(A=\dfrac{1}{2}.\dfrac{2^2}{3}.\dfrac{3^2}{2.4}.\dfrac{4^2}{3.5}...\dfrac{2016^2}{2015.2017}\)
\(A=\left(\dfrac{2.3.4...2016}{2.3.4.5...2015}\right).\left(\dfrac{2.3.4...2016}{2.3.4.5...2017}\right)\)
\(A=2016.\dfrac{1}{2017}=\dfrac{2016}{2017}\)

Lời giải:
Xét tổng quát:
\(1+\frac{1}{k(k+2)}=\frac{k(k+2)+1}{k(k+2)}=\frac{(k+1)^2}{k(k+2)}\)
Thay $k=1,2,....,2015$ ta có:
\(1+\frac{1}{1.3}=\frac{2^2}{1.3}\)
\(1+\frac{1}{2.4}=\frac{3^2}{2.4}\)
\(1+\frac{1}{3.5}=\frac{4^2}{3.5}\)
\(1+\frac{1}{4.6}=\frac{5^2}{4.6}\)
.............
\(1+\frac{1}{2015.2017}=\frac{2016^2}{2015.2017}\)
Nhân theo vế:
\(\Rightarrow A=\frac{1}{2}\left(1+\frac{1}{1.3}\right)\left(1+\frac{1}{2.4}\right)\left(1+\frac{1}{3.5}\right)....\left(1+\frac{1}{2015.2017}\right)\)
\(=\frac{1}{2}.\frac{2^2}{1.3}.\frac{3^2}{2.4}.\frac{4^2}{3.5}.\frac{5^2}{4.6}....\frac{2016^2}{2015.2017}\)
\(=\frac{(1.2.3...2016)^2}{(1.2.3...2015)(2.3.4...2017)}=\frac{(1.2.3...2016)(2.3....2016)}{(1.2.3...2015)(2.3.4...2017)}=2016.\frac{1}{2017}=\frac{2016}{2017}\)

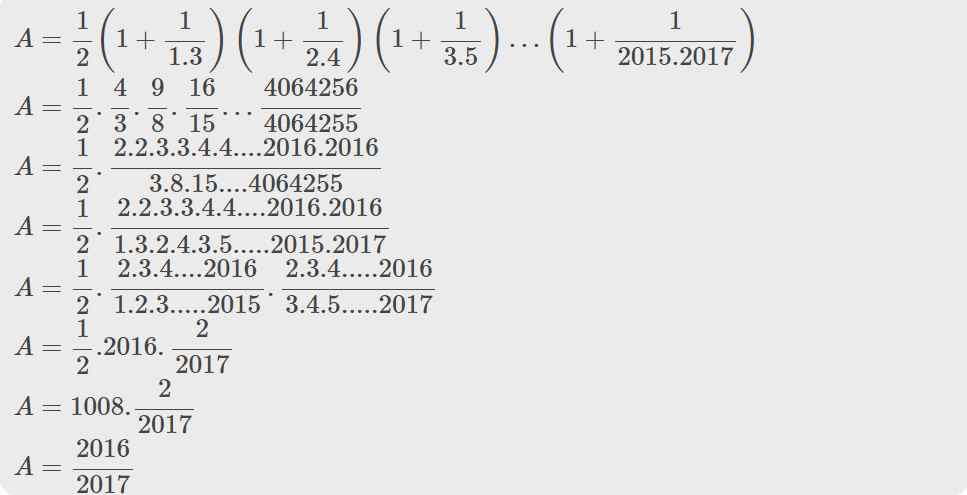
\(A=\dfrac{1}{2}\left(1+\dfrac{1}{1.3}\right)\left(1+\dfrac{1}{2.4}\right)\left(1+\dfrac{1}{3.5}\right)...\left(1+\dfrac{1}{2015.2017}\right)\)\(A=\dfrac{1}{2}.\dfrac{4}{3}.\dfrac{9}{8}.\dfrac{16}{15}...\dfrac{4064256}{4064255}\)
\(A=\dfrac{1}{2}.\dfrac{2.2.3.3.4.4....2016.2016}{3.8.15....4064255}\)
\(A=\dfrac{1}{2}.\dfrac{2.2.3.3.4.4....2016.2016}{1.3.2.4.3.5.....2015.2017}\)
\(A=\dfrac{1}{2}.\dfrac{2.3.4....2016}{1.2.3.....2015}.\dfrac{2.3.4.....2016}{3.4.5.....2017}\)
\(A=\dfrac{1}{2}.2016.\dfrac{2}{2017}\)
\(A=1008.\dfrac{2}{2017}\)
\(A=\dfrac{2016}{2017}\)

\(A=\dfrac{1}{2}.\left(1+\dfrac{1}{1.3}\right)\left(1+\dfrac{1}{2.4}\right)\left(1+\dfrac{1}{3.5}\right)....\left(\dfrac{1}{2015.2017}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1}.\dfrac{2}{3}\right).\left(\dfrac{3}{2}.\dfrac{3}{4}\right).\left(\dfrac{4}{3}.\dfrac{4}{5}\right)....\left(\dfrac{2016}{2015}.\dfrac{2016}{2017}\right)\)
\(=\dfrac{1}{2}.\left(\dfrac{2}{1}.\dfrac{2}{3}\right).\left(\dfrac{3}{2}.\dfrac{3}{4}\right).\left(\dfrac{4}{3}.\dfrac{4}{5}\right).....\left(\dfrac{2016}{2015}.\dfrac{2016}{2017}\right)\)
\(=\dfrac{2016}{2017}\)

P = (1 + \(\dfrac{1}{1.3}\)).(1 + \(\dfrac{1}{2.4}\)).(1 + \(\dfrac{1}{3.5}\))....(1 + \(\dfrac{1}{2020.2022}\))
P = \(\dfrac{1.3+1}{1.3}\). \(\dfrac{2.4+1}{2.4}\).\(\dfrac{3.5+1}{3.5}\)....\(\dfrac{2020.2022+1}{2020.2022}\)
P=\(\dfrac{\left(2-1\right)\left(2+1\right)+1}{1.3}\).\(\dfrac{\left(3-1\right)\left(3+1\right)+1}{2.4}\)...\(\dfrac{\left(2021+1\right).\left(2022-1\right)+1}{2020.2022}\)
P = \(\dfrac{2.2}{1.3}\).\(\dfrac{3.3}{2.4}\).\(\dfrac{4.4}{3.5}\)....\(\dfrac{2021.2021}{2020.2022}\)
P = \(\dfrac{2.2021}{2022}\)
P = \(\dfrac{2021}{1011}\)

\(=\dfrac{1}{2}\cdot\dfrac{2^2-1+1}{\left(2-1\right)\left(2+1\right)}\cdot\dfrac{3^2-1+1}{\left(3-1\right)\left(3+1\right)}\cdot...\cdot\dfrac{2016^2-1+1}{\left(2016-1\right)\left(2016+1\right)}\)
\(=\dfrac{1}{2}\cdot\dfrac{2}{1}\cdot\dfrac{3}{2}\cdot...\cdot\dfrac{2016}{2015}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}\cdot...\cdot\dfrac{2016}{2017}\)
\(=\dfrac{1}{2}\cdot2016\cdot\dfrac{2}{2017}=\dfrac{2016}{2017}\)

P = (1+\(\dfrac{1}{1.3}\)).(1+\(\dfrac{1}{2.4}\)).(1 + \(\dfrac{1}{3.5}\))...(1+\(\dfrac{1}{2020.2022}\))
P =\(\dfrac{1.3+1}{1.3}\).\(\dfrac{2.4+1}{2.4}\).\(\dfrac{3.5+1}{3.5}\)...\(\dfrac{2020.2022+1}{2020.2022}\)
P = \(\dfrac{(2-1)(2+1)+1}{1.3}\).\(\dfrac{(3-1)(3+1)+1}{2.4}\)...\(\dfrac{(2021-1)(2021+1)}{2020.2022}\)
P = \(\dfrac{2.2}{1.3}\).\(\dfrac{3.3}{2.4}\).\(\dfrac{4.4}{3.5}\)...\(\dfrac{2021.2021}{2020.2022}\)
P = \(\dfrac{2021}{1011}\)
\(A=\dfrac{1}{2}\left(\dfrac{2.2}{1.3}\right).\left(\dfrac{3.3}{2.4}\right)...\left(\dfrac{2020.2020}{2019.2021}\right)\)
\(=\dfrac{1.2.2.3.3...2020.2020}{1.2.2.3.3.4.4...2019.2021}\)
\(=\dfrac{1}{2021}\)
\(A=\dfrac{1}{2}\cdot\left(1+\dfrac{1}{1\cdot3}\right)\left(1+\dfrac{1}{2\cdot4}\right)\left(1+\dfrac{1}{3\cdot5}\right)...\left(1+\dfrac{1}{2019\cdot2021}\right)\)
\(A=\dfrac{1}{2}\left(1+\dfrac{1}{2^2-1}\right)\left(1+\dfrac{1}{3^2-1}\right)\left(1+\dfrac{1}{4^2-1}\right)...\left(1+\dfrac{1}{2020^2-1}\right)\)
\(A=\dfrac{1}{2}\cdot\dfrac{2^2}{\left(2-1\right)\left(2+1\right)}\cdot\dfrac{3^2}{\left(3-1\right)\cdot\left(3+1\right)}...\left(\dfrac{2020^2}{\left(2020-1\right)\cdot\left(2020+1\right)}\right)\)
\(A=\dfrac{1}{2}\cdot\dfrac{2}{1}\cdot\dfrac{2}{3}\cdot\dfrac{3}{2}\cdot\dfrac{3}{4}\cdot...\cdot\dfrac{2020}{2019}\cdot\dfrac{2020}{2021}\)
\(A=\dfrac{1}{2}\cdot\dfrac{2}{1}\cdot\dfrac{3}{2}\cdot...\cdot\dfrac{2020}{2019}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}\cdot...\cdot\dfrac{2020}{2021}\)
\(A=\dfrac{1}{2}\cdot2020\cdot\dfrac{2}{2021}=\dfrac{2020}{2021}\)