Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đặt \(A=\frac{1}{2}+\left(\frac{1}{2}\right)^2+\left(\frac{1}{2}\right)^3+...+\left(\frac{1}{2}\right)^{20}\)(1)
\(\Rightarrow2A=1+\frac{1}{2}+\left(\frac{1}{2}\right)^2+...+\left(\frac{1}{2}\right)^{19}\)(2)
Lấy (2) trừ đi (1) ta có :
\(\Rightarrow2A-A=1-\left(\frac{1}{2}\right)^{20}\)
\(\Rightarrow A=1-\left(\frac{1}{2}\right)^{20}\)

\(\frac{1}{2}S=\left(\frac{1}{2}\right)^2+\left(\frac{1}{2}\right)^3+...+\left(\frac{1}{2}\right)^{21}\)
\(\Rightarrow\left(\frac{1}{2}S\right)-S=\left(\left(\frac{1}{2}\right)^2+\left(\frac{1}{2}\right)^3+...+\left(\frac{1}{2}\right)^{21}\right)-\left(\left(\frac{1}{2}\right)+\left(\frac{1}{2}\right)^2+...+\left(\frac{1}{2}\right)^{20}\right)\)
\(\Rightarrow-\frac{1}{2}S=\left(\frac{1}{2}\right)^{21}-\left(\frac{1}{2}\right)\)
\(\Rightarrow S=\frac{\left(\left(\frac{1}{2}\right)^{21}-\frac{1}{2}\right)}{-\frac{1}{2}}\)

(x + 20)⁴ + (2y - 1)²⁰²⁴ ≤ 0
⇒ (x + 20)⁴ = 0 và (2y - 1)²⁰²⁴ = 0
*) (x + 20)⁴ = 0
x + 20 = 0
x = 0 - 20
x = -20
*) (2y - 1)²⁰²⁴ = 0
2y - 1 = 0
2y = 1
y = 1/2
M = 5.(-20)².1/2 - 4.(-2).(1/2)²
= 1000 + 2
= 1002

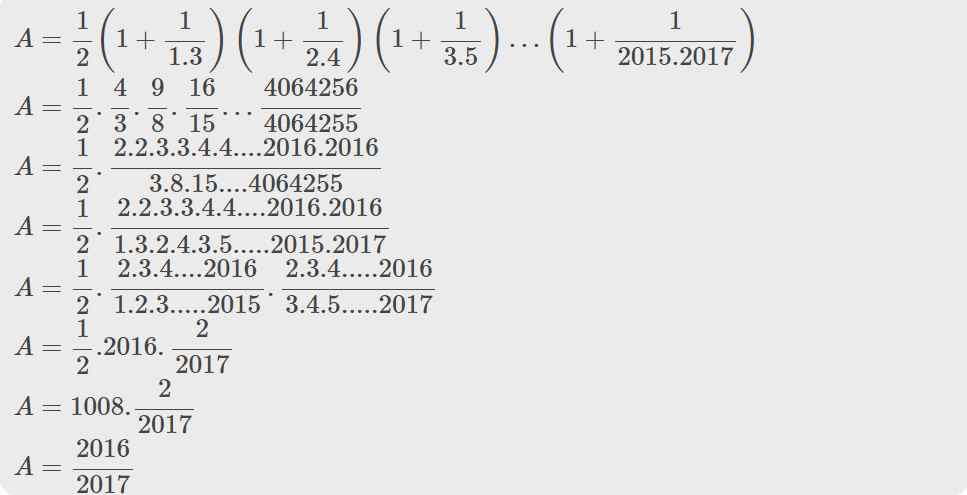
\(A=\dfrac{1}{2}.\left(1+\dfrac{1}{1.3}\right)\left(1+\dfrac{1}{2.4}\right)\left(1+\dfrac{1}{3.5}\right)....\left(\dfrac{1}{2015.2017}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1}.\dfrac{2}{3}\right).\left(\dfrac{3}{2}.\dfrac{3}{4}\right).\left(\dfrac{4}{3}.\dfrac{4}{5}\right)....\left(\dfrac{2016}{2015}.\dfrac{2016}{2017}\right)\)
\(=\dfrac{1}{2}.\left(\dfrac{2}{1}.\dfrac{2}{3}\right).\left(\dfrac{3}{2}.\dfrac{3}{4}\right).\left(\dfrac{4}{3}.\dfrac{4}{5}\right).....\left(\dfrac{2016}{2015}.\dfrac{2016}{2017}\right)\)
\(=\dfrac{2016}{2017}\)
tổng đó bằng 3,5