Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Ta có: \(\sqrt{\left(2-\sqrt{3}\right)^2}+\dfrac{2}{\sqrt{3}+1}-6\sqrt{\dfrac{16}{3}}\)
\(=2-\sqrt{3}+\sqrt{3}-1-6\cdot\dfrac{4}{\sqrt{3}}\)
\(=1-8\sqrt{3}\)

a ) \(2\sqrt{45}+\sqrt{5}-3\sqrt{80}\)
= \(2\sqrt{9.5}+\sqrt{5}-3\sqrt{16.5}\) \
= \(2.3\sqrt{5}+\sqrt{5}-3.4\sqrt{5}\)
= \(6\sqrt{5}+\sqrt{5}-12\sqrt{5}\)
= \(\left(6+1-12\right)\sqrt{5}\)
= \(-5\sqrt{5}\)
b ) \(\sqrt{\left(2-\sqrt{3}\right)^2}+\dfrac{2}{\sqrt{3}+1}-6\sqrt{\dfrac{16}{3}}\)
= / \(2-\sqrt{3}\) / \(+\dfrac{2.\left(\sqrt{3}-1\right)}{\left(\sqrt{3}+1\right).\left(\sqrt{3}-1\right)}-6\sqrt{\dfrac{48}{3^2}}\)
= \(2-\sqrt{3}+\dfrac{2.\left(\sqrt{3}-1\right)}{\sqrt{3}^2-1^2}-\dfrac{6}{3}\sqrt{48}\)
= \(2-\sqrt{3}+\dfrac{2.\left(\sqrt{3}-1\right)}{3-1}-2\sqrt{48}\)
=\(2-\sqrt{3}+\sqrt{3}-1-2\sqrt{16.3}\)
= \(2-\sqrt{3}+\sqrt{3}-1-8\sqrt{3}\)
= \(1-8\sqrt{3}\)
ý c ) em không biết làm ☹

a) Ta có: \(2\sqrt{80}+3\sqrt{45}-\sqrt{245}\)
\(=8\sqrt{5}+9\sqrt{5}-7\sqrt{5}\)
\(=10\sqrt{5}\)
b) Ta có: \(\dfrac{3}{2+\sqrt{3}}+\dfrac{13}{4-\sqrt{3}}+\dfrac{6}{\sqrt{3}}\)
\(=3\left(2-\sqrt{3}\right)+4+\sqrt{3}+2\sqrt{3}\)
\(=6-2\sqrt{3}+4+3\sqrt{3}\)
\(=10+\sqrt{3}\)
c) Ta có: \(\left(\dfrac{\sqrt{14}-\sqrt{7}}{\sqrt{2}-1}+\dfrac{\sqrt{15}-\sqrt{5}}{\sqrt{3}-1}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
\(=\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)\)
=7-5=2
d) Ta có: \(\sqrt{\left(2+\sqrt{3}\right)^2}-\sqrt{28-10\sqrt{3}}\)
\(=2+\sqrt{3}-5+\sqrt{3}\)
\(=-3+2\sqrt{3}\)
a. \(2\sqrt{80}+3\sqrt{45}-\sqrt{245}\)
\(=2.4\sqrt{5}+3.3\sqrt{5}-7\sqrt{5}\)
\(=8\sqrt{5}+9\sqrt{5}-7\sqrt{5}\)
\(=10\sqrt{5}\)
b. \(\dfrac{3}{2+\sqrt{3}}+\dfrac{13}{4-\sqrt{3}}+\dfrac{6}{\sqrt{3}}\)
\(=\dfrac{3\left(2-\sqrt{3}\right)}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}+\dfrac{13\left(4+\sqrt{3}\right)}{\left(4-\sqrt{3}\right)\left(4+\sqrt{3}\right)}+\dfrac{6\sqrt{3}}{\sqrt{3}.\sqrt{3}}\)
\(=\dfrac{3\left(2-\sqrt{3}\right)}{4-3}+\dfrac{13\left(4+\sqrt{3}\right)}{16-3}+\dfrac{6\sqrt{3}}{3}\)
\(=3\left(2-\sqrt{3}\right)+\dfrac{13\left(4+\sqrt{3}\right)}{13}+2\sqrt{3}\)
\(=6-3\sqrt{3}+4+\sqrt{3}+2\sqrt{3}\)
\(=10\)
c. \(\left(\dfrac{\sqrt{14}-\sqrt{7}}{\sqrt{2}-1}+\dfrac{\sqrt{15}-\sqrt{5}}{\sqrt{3}-1}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
\(=\left(\dfrac{\sqrt{7}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}+\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\right).\left(\sqrt{7}-\sqrt{5}\right)\)
\(=\left(\sqrt{7}+\sqrt{5}\right).\left(\sqrt{7}-\sqrt{5}\right)\)
\(=7-5=2\)
d. \(\sqrt{\left(2+\sqrt{3}\right)^2}-\sqrt{28-10\sqrt{3}}\)
\(=\left|2+\sqrt{3}\right|-\sqrt{5^2-2.5.\sqrt{3}+\left(\sqrt{3}\right)^2}\)
\(=\left|2+\sqrt{3}\right|-\left(5-\sqrt{3}\right)^2\)
\(=\left|2+\sqrt{3}\right|-\left|5-\sqrt{3}\right|\)
\(=2+\sqrt{3}-\left(5-\sqrt{3}\right)\) (vì \(\left|2+\sqrt{3}\right|\ge0,\left|5-\sqrt{3}\right|\ge0\))
\(=2+\sqrt{3}-5+\sqrt{3}\)
\(=2\sqrt{3}-3\)

Lời giải:
a.
\(=2\sqrt{4^2.5}+3\sqrt{3^2.5}-\sqrt{7^2.5}=2.4\sqrt{5}+3.3\sqrt{5}-7\sqrt{5}\)
\(=8\sqrt{5}+9\sqrt{5}-7\sqrt{5}=10\sqrt{5}\)
b.
\(=\frac{3(2-\sqrt{3})}{(2-\sqrt{3})(2+\sqrt{3})}+\frac{13(4+\sqrt{3})}{(4-\sqrt{3})(4+\sqrt{3})}+\frac{6\sqrt{3}}{3}\)
\(=\frac{6-3\sqrt{3}}{1}+\frac{13(4+\sqrt{3})}{13}+2\sqrt{3}=6-3\sqrt{3}+4+\sqrt{3}+2\sqrt{3}\)
\(=10\)
c.
\(=\left[\frac{\sqrt{7}(\sqrt{2}-1)}{\sqrt{2}-1}+\frac{\sqrt{5}(\sqrt{3}-1)}{\sqrt{3}-1}\right].(\sqrt{7}-\sqrt{5})\)
\(=(\sqrt{7}+\sqrt{5})(\sqrt{7}-\sqrt{5})=7-5=2\)
d.
\(=|2+\sqrt{3}|-\sqrt{5^2-2.5\sqrt{3}+3}=|2+\sqrt{3}|-\sqrt{(5-\sqrt{3})^2}\)
\(=|2+\sqrt{3}|-|5-\sqrt{3}|=2+\sqrt{3}-(5-\sqrt{3})=-3+2\sqrt{3}\)

a) \(\dfrac{2\sqrt{125}-3\sqrt{5}-\sqrt{180}}{-\sqrt{5}}+\sqrt{8}=\dfrac{2\sqrt{25.5}-3\sqrt{5}-\sqrt{36.5}}{-\sqrt{5}}+\sqrt{8}\)
\(=\dfrac{10\sqrt{5}-3\sqrt{5}-6\sqrt{5}}{-\sqrt{5}}+2\sqrt{2}=\dfrac{\sqrt{5}}{-\sqrt{5}}+2\sqrt{2}=2\sqrt{2}-1\)
b) \(\sqrt{\left(\sqrt{2}-\sqrt{3}\right)^2}+\sqrt{18}=\left|\sqrt{2}-\sqrt{3}\right|+\sqrt{9.2}\)
\(=\sqrt{3}-\sqrt{2}+3\sqrt{2}=2\sqrt{2}+\sqrt{3}\)
c) \(\sqrt{48}-6\sqrt{\dfrac{1}{3}}+\dfrac{\sqrt{3}-3}{\sqrt{3}}=\sqrt{16.3}-2\sqrt{9.\dfrac{1}{3}}+\dfrac{\sqrt{3}\left(1-\sqrt{3}\right)}{\sqrt{3}}\)
\(=4\sqrt{3}-2\sqrt{3}+1-\sqrt{3}=1+\sqrt{3}\)
d) \(\left(\dfrac{\sqrt{6}-\sqrt{2}}{1-\sqrt{3}}-\dfrac{5}{\sqrt{5}}\right):\dfrac{1}{\sqrt{5}-\sqrt{2}}=\left(\dfrac{\sqrt{2}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}-\sqrt{5}\right).\left(\sqrt{5}-\sqrt{2}\right)\)
\(=\left(-\sqrt{2}-\sqrt{5}\right)\left(\sqrt{5}-\sqrt{2}\right)=-\left(\sqrt{5}+\sqrt{2}\right)\left(\sqrt{5}-\sqrt{2}\right)=-3\)

\(A=\left(2+\dfrac{5-2\sqrt{5}}{2-\sqrt{5}}\right)\left(2+\dfrac{5+3\sqrt{5}}{3+\sqrt{5}}\right)\)
\(A=\left[2-\dfrac{\sqrt{5}\left(\sqrt{5}-2\right)}{\sqrt{5}-2}\right]\left[2+\dfrac{\sqrt{5}\left(\sqrt{5}+3\right)}{\sqrt{5}+3}\right]\)
\(A=\left(2-\sqrt{5}\right)\left(2+\sqrt{5}\right)\)
\(A=2^2-\left(\sqrt{5}\right)^2\)
\(A=4-5\)
\(A=-1\)
____
\(B=\left(\dfrac{15}{\sqrt{6}+1}+\dfrac{4}{\sqrt{6}-2}-\dfrac{12}{3-\sqrt{6}}\right)\left(\sqrt{6}+11\right)\)
\(B=\left[\dfrac{15\left(\sqrt{6}-1\right)}{\left(\sqrt{6}+1\right)\left(\sqrt{6}-1\right)}+\dfrac{4\left(\sqrt{6}+2\right)}{\left(\sqrt{6}-2\right)\left(\sqrt{6}+2\right)}-\dfrac{12\left(3+\sqrt{6}\right)}{\left(3+\sqrt{6}\right)\left(3-\sqrt{6}\right)}\right]\left(\sqrt{6}+11\right)\)
\(B=\left[\dfrac{15\left(\sqrt{6}-1\right)}{5}+\dfrac{4\left(\sqrt{6}+2\right)}{2}-\dfrac{12\left(3+\sqrt{6}\right)}{3}\right]\left(\sqrt{6}+11\right)\)
\(B=\left(3\sqrt{6}-3+2\sqrt{6}+4-12-4\sqrt{6}\right)\left(\sqrt{6}+11\right)\)
\(B=\left(\sqrt{6}-11\right)\left(\sqrt{6}+11\right)\)
\(B=6-121\)
\(B=-115\)

a) Ta có: \(-\dfrac{3}{2}\sqrt{9-4\sqrt{5}}+\sqrt{\left(-4\right)^2\cdot\left(1+\sqrt{5}\right)^2}\)
\(=\dfrac{-3}{2}\left(\sqrt{5}-2\right)+4\cdot\left(\sqrt{5}+1\right)\)
\(=\dfrac{-3}{2}\sqrt{5}+3+4\sqrt{5}+4\)
\(=\dfrac{5}{2}\sqrt{5}+7\)
b) Ta có: \(\left(1+\dfrac{1}{\tan^225^0}\right)\cdot\sin^225^0-\tan55^0\cdot\tan35^0\)
\(=\dfrac{\tan^225^0+1}{\tan^225^0}\cdot\sin25^0-1\)
\(=\left(\dfrac{\sin^225^0}{\cos^225^0}+1\right)\cdot\dfrac{\cos^225^0}{\sin^225^0}\cdot\sin25^0-1\)
\(=\dfrac{\sin^225^0+\cos^225^0}{\cos^225^0}\cdot\dfrac{\cos^225^0}{\sin25^0}-1\)
\(=\dfrac{1}{\sin25^0}-1\)
\(=\dfrac{1-\sin25^0}{\sin25^0}\)

j.
\(J=\left[\frac{1}{\sqrt{(\sqrt{5}-\sqrt{2})^2}}-\frac{\sqrt{2}}{\sqrt{2}(\sqrt{5}+\sqrt{2})}+1\right].\frac{1}{(\sqrt{2}+1)^2}\)
\(=\left(\frac{1}{\sqrt{5}-\sqrt{2}}-\frac{1}{\sqrt{5}+\sqrt{2}}+1\right).\frac{1}{(\sqrt{2}+1)^2}\)
\(=[\frac{\sqrt{5}+\sqrt{2}-(\sqrt{5}-\sqrt{2})}{(\sqrt{5}-\sqrt{2})(\sqrt{5}+\sqrt{2})}+1].\frac{1}{(\sqrt{2}+1)^2}=(\frac{2\sqrt{2}}{3}+1).\frac{1}{(\sqrt{2}+1)^2}=\frac{3+2\sqrt{2}}{3}.\frac{1}{3+2\sqrt{2}}=\frac{1}{3}\)
k. Đề sai sai, bạn xem lại
o.
\(O=(4+\sqrt{15})(\sqrt{5}-\sqrt{3}).\sqrt{2}.\sqrt{4-\sqrt{15}}\)
\(=(4+\sqrt{15}(\sqrt{5}-\sqrt{3})\sqrt{8-2\sqrt{15}}=(4+\sqrt{15})(\sqrt{5}-\sqrt{3})\sqrt{(\sqrt{5}-\sqrt{3})^2}\)
\(=(4+\sqrt{15})(\sqrt{5}-\sqrt{3})(\sqrt{5}-\sqrt{3})=(4+\sqrt{15})(8-2\sqrt{15})\)
\(=2(4+\sqrt{15})(4-\sqrt{15})=2(16-15)=2\)
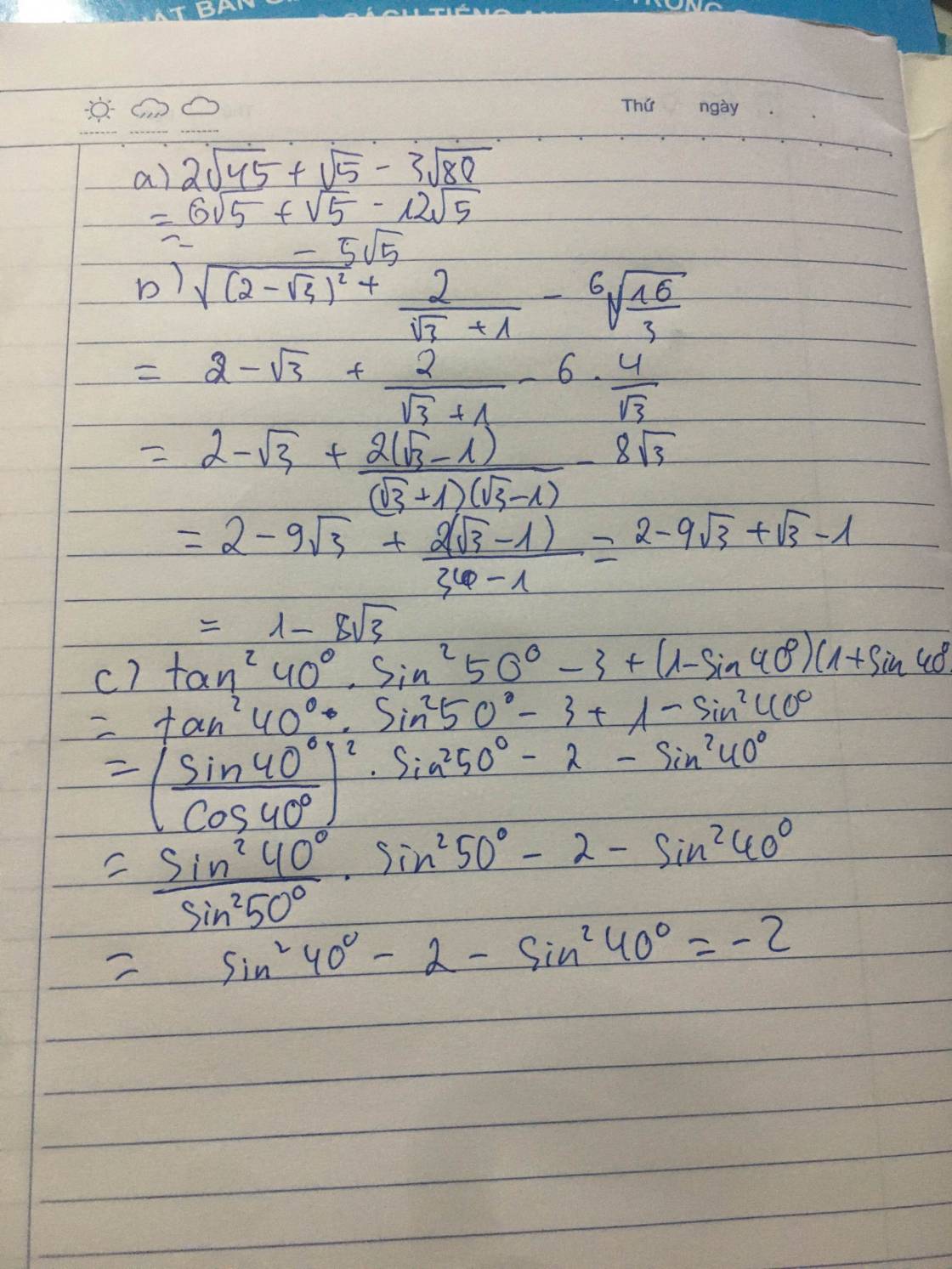
a: \(2\sqrt{45}+\sqrt{5}-3\sqrt{80}\)
\(=6\sqrt{5}+\sqrt{5}-12\sqrt{5}\)
\(=-5\sqrt{5}\)
b: \(\sqrt{\left(2-\sqrt{3}\right)^2}+\dfrac{2}{\sqrt{3}+1}-6\sqrt{\dfrac{16}{3}}\)
\(=2-\sqrt{3}+\sqrt{3}-1-8\sqrt{3}\)
\(=-8\sqrt{3}+1\)