Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{8^{14}}{4^4.64^5}=\dfrac{\left(2^3\right)^{14}}{\left(2^2\right)^4.\left(2^5\right)^5}=\dfrac{2^{42}}{2^8.2^{25}}=2^{42-\left(8+25\right)}=2^9\)
\(\dfrac{9^{10}.27^7}{81^7.3^{15}}=\dfrac{\left(3^2\right)^{10}.\left(3^3\right)^7}{\left(3^4\right)^7.3^{15}}=\dfrac{3^{20}.3^{21}}{3^{28}.3^{15}}=\dfrac{3^{20+21}}{3^{28+15}}=\dfrac{3^{41}}{3^{41}.3^2}=\dfrac{1}{3^2}=\dfrac{1}{9}\)

\(A=\left(3-\dfrac{1}{4}+\dfrac{3}{2}\right)-\left(5+\dfrac{1}{3}-\dfrac{5}{6}\right)-\left(6-\dfrac{7}{4}+\dfrac{2}{3}\right)\\ \Rightarrow A=3-\dfrac{1}{4}+\dfrac{3}{2}-5-\dfrac{1}{3}+\dfrac{5}{6}-6+\dfrac{7}{4}-\dfrac{2}{3}\\ \Rightarrow A=\left(3-5-6\right)-\left(\dfrac{1}{4}+\dfrac{7}{4}\right)+\left(\dfrac{3}{2}+\dfrac{5}{6}-\dfrac{2}{3}\right)\\ \Rightarrow A=-8-\dfrac{3}{2}+\dfrac{5}{3}\\ =-\dfrac{47}{6}.\\ B=0,5+\dfrac{1}{3}+0,4+\dfrac{5}{7}+\dfrac{1}{6}-\dfrac{4}{35}+\dfrac{1}{41}\)
\(\Rightarrow B=\left(0,5+0,4\right)+\left(\dfrac{1}{3}+\dfrac{1}{6}\right)+\left(\dfrac{5}{7}-\dfrac{4}{35}\right)+\dfrac{1}{41}\\ \Rightarrow B=\dfrac{9}{10}+\dfrac{1}{2}+\dfrac{3}{5}+\dfrac{1}{41}\\ \Rightarrow B=2+\dfrac{1}{41}\\ \Rightarrow B=\dfrac{83}{41}.\)

\(\dfrac{4^5\cdot9^4}{8^3\cdot27^3}=\dfrac{\left(2^2\right)^5\cdot\left(3^2\right)^4}{\left(2^3\right)^3\cdot\left(3^3\right)^3}=\dfrac{2^{10}\cdot3^8}{2^9\cdot3^9}=\dfrac{2}{3}\)
\(\dfrac{4^{20}\cdot3^{35}}{2^{37}\cdot27^{12}}=\dfrac{\left(2^2\right)^{20}\cdot3^{35}}{2^{37}\cdot\left(3^3\right)^{12}}=\dfrac{2^{40}\cdot3^{35}}{2^{37}\cdot3^{36}}=\dfrac{2^3}{3}\)
\(\dfrac{5^4\cdot20^4}{25^5\cdot4^5}=\dfrac{5^4\cdot5^4\cdot4^4}{5^5\cdot5^5\cdot4^5}=\dfrac{1}{5^2\cdot4}=\dfrac{1}{100}\)
\(\dfrac{2^{15}\cdot9^4}{6^6\cdot8^3}=\dfrac{2^{15}\cdot\left(3^2\right)^4}{2^6\cdot3^6\cdot\left(2^3\right)^3}=\dfrac{2^{15}\cdot3^8}{2^6\cdot3^6\cdot2^9}=3^2\)

\(=\dfrac{2^{19}\cdot3^9-3\cdot3^8\cdot2^{18}\cdot5}{2^{19}\cdot3^9+2^{20}\cdot3^{10}}=\dfrac{-3^{10}\cdot2^{18}}{2^{19}\cdot3^9\cdot7}=-\dfrac{3}{14}\)

\(\dfrac{2^{15}.9^4}{6^6.8^3}=\dfrac{2^{15}.3^8}{2^6.3^6.2^9}=\dfrac{2^{15}.3^8}{2^{15}.3^6}=3^2=9\)

a: \(A=1-\dfrac{2\left(25-\dfrac{2}{2018}+\dfrac{1}{2019}-\dfrac{1}{2020}\right)}{4\left(25-\dfrac{2}{2018}+\dfrac{1}{2019}-\dfrac{1}{2020}\right)}\)
=1-2/4=1/2
b: \(B=\dfrac{5^{10}\cdot7^3-5^{10}\cdot7^4}{5^9\cdot7^3+5^9\cdot7^3\cdot2^3}\)
\(=\dfrac{5^{10}\cdot7^3\left(1-7\right)}{5^9\cdot7^3\left(1+2^3\right)}=5\cdot\dfrac{-6}{9}=-\dfrac{10}{3}\)
c: x-y=0 nên x=y
\(C=x^{2020}-x^{2020}+y\cdot y^{2019}-y^{2019}\cdot y+2019\)
=2019

Ta có: \(M=\dfrac{\dfrac{1}{99}+\dfrac{2}{98}+\dfrac{3}{97}+\dfrac{4}{96}+...+\dfrac{97}{3}+\dfrac{98}{2}+\dfrac{99}{1}}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+...+\dfrac{1}{100}}\)
\(=\dfrac{\left(1+\dfrac{1}{99}\right)+\left(1+\dfrac{2}{98}\right)+\left(1+\dfrac{3}{97}\right)+\left(1+\dfrac{4}{96}\right)+...+\left(1+\dfrac{98}{2}\right)+1}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+...+\dfrac{1}{100}}\)
\(=\dfrac{\dfrac{100}{99}+\dfrac{100}{98}+\dfrac{100}{97}+...+\dfrac{100}{1}+\dfrac{100}{2}}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+...+\dfrac{1}{100}}\)
=100
Ta có: \(N=\dfrac{92-\dfrac{1}{9}-\dfrac{2}{10}-\dfrac{3}{11}-...-\dfrac{90}{98}-\dfrac{91}{99}-\dfrac{92}{100}}{\dfrac{1}{45}+\dfrac{1}{50}+\dfrac{1}{55}+...+\dfrac{1}{495}+\dfrac{1}{500}}\)
\(=\dfrac{\left(1-\dfrac{1}{9}\right)+\left(1-\dfrac{2}{10}\right)+\left(1-\dfrac{3}{11}\right)+...+\left(1-\dfrac{90}{98}\right)+\left(1-\dfrac{91}{99}\right)+\left(1-\dfrac{92}{100}\right)}{\dfrac{1}{5}\left(\dfrac{1}{9}+\dfrac{1}{10}+\dfrac{1}{11}+...+\dfrac{1}{99}+\dfrac{1}{100}\right)}\)
\(=\dfrac{\dfrac{8}{9}+\dfrac{8}{10}+\dfrac{8}{11}+...+\dfrac{8}{99}+\dfrac{8}{100}}{\dfrac{1}{5}\left(\dfrac{1}{9}+\dfrac{1}{10}+\dfrac{1}{11}+...+\dfrac{1}{99}+\dfrac{1}{100}\right)}\)
\(=\dfrac{8}{\dfrac{1}{5}}=40\)
\(\Leftrightarrow\dfrac{M}{N}=\dfrac{100}{40}=\dfrac{5}{2}\)
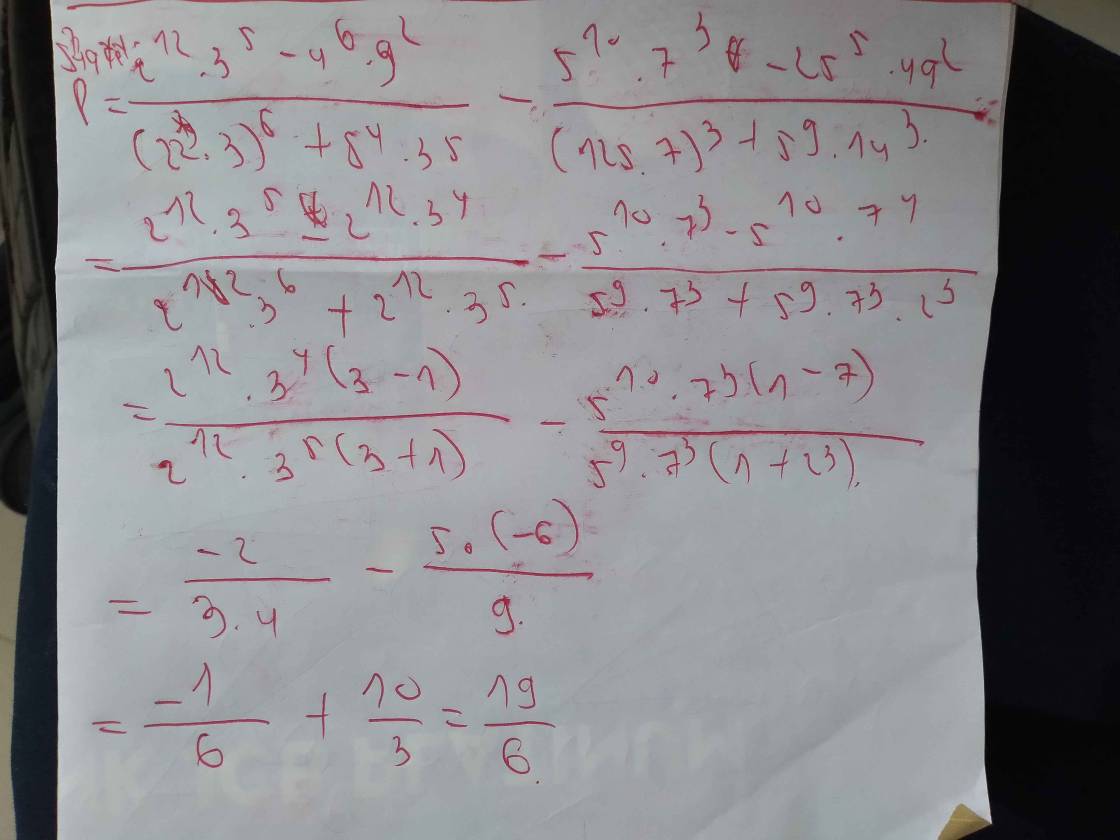
`@` `\text {Ans}`
`\downarrow`
\(\dfrac{2^8-2^3}{2^5-1}=\dfrac{2^3\left(2^5-1\right)}{2^5-1}=\dfrac{2^3}{1}=2^3=8\)
_____
\(\dfrac{4^8\cdot9^4}{6^6\cdot8^3}\)
`=`\(\dfrac{\left(2^2\right)^8\cdot\left(3^2\right)^4}{2^6\cdot3^6\cdot\left(2^3\right)^3}\)
`=`\(\dfrac{2^{16}\cdot3^8}{2^6\cdot3^6\cdot2^9}\)
`=`\(\dfrac{2^{16}\cdot3^8}{2^{15}\cdot3^6}\)
`=`\(\dfrac{3^2}{2}\) `=`\(\dfrac{9}{2}\)
______
\(\dfrac{27^4\cdot2^3-3^{10}\cdot4^3}{6^4\cdot9^3}\)
`=`\(\dfrac{\left(3^3\right)^4\cdot2^3-3^{10}\cdot\left(2^2\right)^3}{2^4\cdot3^4\cdot\left(3^2\right)^3}\)
`=`\(\dfrac{3^{12}\cdot2^3-3^{10}\cdot2^6}{2^4\cdot3^4\cdot3^6}\)
`=`\(\dfrac{3^{10}\cdot\left(3^2\cdot2^3-2^6\right)}{3^{10}\cdot2^4}\)
`=`\(\dfrac{72-2^6}{2^4}=\dfrac{8}{16}=\dfrac{1}{2}\)
\(\dfrac{2^8-2^3}{2^5-1}=\dfrac{2^3\left(2^5-1\right)}{2^5-1}=2^3=8\)
\(\dfrac{4^8.9^4}{6^6.8^3}=\dfrac{2^{16}.3^8}{2^6.3^6.2^9}=2.3^2=18\)
\(\dfrac{27^4.2^3-3^{10}.4^3}{6^4.9^3}=\dfrac{3^{12}.2^3-3^{10}.2^6}{2^4.3^4.3^6}=\dfrac{2^3.3^{10}.\left(3^2-2^3\right)}{2^4.3^{10}}=\dfrac{9-8}{2}=\dfrac{1}{2}\)