Tính: C = 2010 1 + 2009 2 + 2008 3...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

15 tháng 10 2018

Tính:

C = 2010 1 + 2009 2 + 2008 3 + . . . + 1 2010 1 2 + 1 3 + 1 4 + . . . + 1 2011

#Toán lớp 6

Cao Minh Tâm

15 tháng 10 2018

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

ngo tien dung

19 tháng 3 2017 - olm

tính C=2010/1+2009/2 + 2008/3 +...+ 1/2010:1\2+1/3+1/4+......+1\2011

#Toán lớp 6

Trần ngọc mai

19 tháng 3 2017

*2010/1+2009/2+...+1/2010

=(2009/2+1)+(2008/3+1)+...+(1/2010+1)+1

=2011/2+2011/3+..+2011/2010+2011/2011

=2011(1/2+1/3+1/4+...+1/2011)

=> C=2011/1=2011

Đúng(0)

Nguyen thi ngoc mai

21 tháng 2 2015 - olm

Cho A = 1/2001+2/2009+3/2008+........2009/+ 2010/1, B = 1+1/2+1/3+1/4+1/5+1/6+.......1/2010+1/2011. Tính A/B

#Toán lớp 6

Nguyễn Phương Uyên

6 tháng 2 2018 - olm

Tính :

\(C=\frac{\frac{2010}{1}+\frac{2009}{2}+\frac{2008}{3}+....+\frac{1}{2010}}{\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+....+\frac{1}{2011}}\)

#Toán lớp 6

Lê Anh Tú

7 tháng 2 2018

Bạn giải cũng được đấy alibaba nguyễn, nhưng theo mình thì làm cách này dễ hiểu hơn!

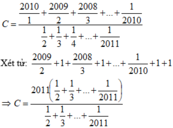
Ta có: \(C=\frac{\frac{2010}{1}+\frac{2009}{2}+\frac{2008}{3}+...+\frac{1}{2010}}{\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2011}}\)

Đặt \(A=\frac{2010}{1}+\frac{2009}{2}+\frac{2008}{3}+...+\frac{1}{2010}\)

\(A=\frac{2010}{1}+1+\frac{2009}{1}+1+\frac{2008}{1}+1+...+\frac{1}{2010}+1-2010\)

\(=\frac{2011}{1}+\frac{2011}{2}+\frac{2011}{3}+...+\frac{2011}{2010}-\frac{2011.2010}{2011}\)

\(=2011\left(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2010}-\frac{2010}{2011}\right)\)

Đặt \(B=\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2011}\)

\(B=1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2011}-1\)

\(=1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2010}-\frac{2010}{2011}\)

Ta có: \(C=\frac{A}{B}=2011\)(lấy A-B)

Đúng(0)

✰๖ۣۜMαĭ Đứ¢ ๖ۣۜMĭηɦ✰ {team 7c}

6 tháng 2 2018

Ta có :

\(2010A=\dfrac{2010^{2012}+2010}{2010^{2012}+1}=\dfrac{2010^{2012}+1+2009}{2010^{2012}+1}=1+\dfrac{2009}{2010^{2012}+1}\)

\(2010B=\dfrac{2010^{2011}+2010}{2010^{2011}+1}=\dfrac{2010^{2011}+1+2009}{2010^{2011}+1}=1+\dfrac{2009}{2010^{2011}+1}\)

Vì \(1+\dfrac{2009}{2010^{2012}+1}< 1+\dfrac{2009}{2010^{2011}+1}\Rightarrow A< B\)

~ Học tốt ~

Đúng(0)

Lê khắc Tuấn Minh

29 tháng 7 2015 - olm

Tinh\(\frac{\frac{2010}{1}+\frac{2009}{2}+\frac{2008}{3}+...+\frac{2}{2009}+\frac{1}{2010}}{\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+...+\frac{1}{2010}+\frac{1}{2011}}\)

#Toán lớp 6

Hồ Thu Giang

29 tháng 7 2015

Ghi lộn đề thiếu thì phải. Hình như thiếu phân số 1/2011

Đúng(0)

Lê Huỳnh Thúy Nga

27 tháng 4 2016 - olm

Bài 5:1/2+1/3+...+1/2008).x=2009/1+2010/2+2011/3+5016/2008-2008

#Toán lớp 6

Lê Đình Đạt

27 tháng 4 2016

tìm x hử

Đúng(0)

Nguyễn Thành Nam

10 tháng 7 2016 - olm

(2008 x 2009 x 2010 x 2011) x (1 + 1/2 : 3/2 - 4/3)

#Toán lớp 6

Le Thi Khanh Huyen

10 tháng 7 2016

(2008 x 2009 x 2010 x 2011) x (1 + 1/2 : 3/2 - 4/3)

=(2008 x 2009 x 2010 x 2011) x (1 + 1/3 - 4/3)

=(2008 x 2009 x 2010 x 2011) x (4/3 - 4/3)

=(2008 x 2009 x 2010 x 2011) x 0

Đúng(0)

cure happy

10 tháng 7 2016

đáp số:0

ủng hộ nha

Đúng(0)

No Name

20 tháng 1 2019 - olm

Tính tổng sau:

(-1)+2+(-3)+4+(-5)+...+2008+(-2009)+2010+(-2011)+2012

#Toán lớp 6

Nguyễn Minh Vũ

20 tháng 1 2019

Ta có dãy số : 1,2,3,...,2011,2012 có : (2012-1)+1=2012(số)

Ta thấy : 2012 :2 nên :

[(-1)+2]+[(-3)+4]+...+[(-2009)+2010]+[(-2011)+2012] (có 1006 cặp)

= 1 . 1006

=1006

Đúng(0)

đào nguyễn việt anh

20 tháng 1 2019

Đặt cả tổng đó là A(hayf j đó tùy bạn)

ta có

A=1+2+3+4+...+2012-2(1+3+5+...+2011)

A=2025078-2.1012036

A=2025078-2024072

A=1006

*xong*

Đúng(0)

Phạm Thùy Dương

24 tháng 10 2015 - olm

Tính giá trị biểu thức : C=1-2-3+4+5-6-7+8+.....+2008+2009-2010-2011+2012

#Toán lớp 6

Vũ Hồng Phúc

6 tháng 4 2020 - olm

1-2-3+4+5-6-7+...+2008+2009-2010-2011

#Toán lớp 6

Uchiha Sasuke

20 tháng 4 2017

Tính:

D =\(\dfrac{\dfrac{2010}{1}+\dfrac{2009}{2}+\dfrac{2008}{3}+...+\dfrac{1}{2010}}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2011}}\)

#Toán lớp 6

Cuber Việt

18 tháng 6 2017

Đặt D1 = \(\dfrac{2010}{1}\) + \(\dfrac{2009}{2}\) + \(\dfrac{2008}{3}\) + ... + \(\dfrac{1}{2010}\)

= 1 + ( 1+ \(\dfrac{2009}{2}\)) + ( 1+ \(\dfrac{2008}{3}\)) + ... + (1+\(\dfrac{1}{2010}\))

= \(\dfrac{2011}{2}\) + \(\dfrac{2011}{3}\)+ ... + \(\dfrac{2011}{2010}\) + \(\dfrac{2011}{2011}\)

= 2011. ( \(\dfrac{1}{2}\) + \(\dfrac{1}{3}\) + ... + \(\dfrac{1}{2010}\) + \(\dfrac{1}{2011}\))

Đặt D2 = \(\dfrac{1}{2}\) + \(\dfrac{1}{3}\) + ... + \(\dfrac{1}{2010}\) + \(\dfrac{1}{2011}\)

=> D = 2011

cho mk 1 tick nha

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP