Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

g)\(=\left(-\dfrac{3}{4}+\dfrac{2}{5}\right).\dfrac{7}{3}+\left(\dfrac{3}{5}+-\dfrac{1}{4}\right).\dfrac{7}{3}\)
\(=\left(-\dfrac{3}{4}+-\dfrac{1}{4}+\dfrac{2}{5}+\dfrac{3}{5}\right).\dfrac{7}{3}\)
\(=\left(-1+1\right).\dfrac{7}{3}=0.\dfrac{7}{3}=0\)
f) \(\dfrac{15^3+5.15^2-5^3}{18^3+6.18^2-6^3}\)
\(=\dfrac{3^3.5^3+5.5^2.3^2-5^3}{3^3.6^3+6.6^2.3^2-6^3}\)
\(=\dfrac{5^3.\left(3^3+3^2-1\right)}{6^3.\left(3^3+3^2-1\right)}\)
\(=\dfrac{5^3}{6^3}\)
\(=\dfrac{125}{216}\)



\(15^3+5.15^2-5^3.\frac{1}{8}^3+6.18^2-6^3\)
\(=15^2.\left(15+5\right)-\left(5.\frac{1}{8}\right)^3+6.\left(18^2-6^2\right)\)
\(=225.20-\left(\frac{5}{8}\right)^3+6.\left(324-36\right)\)
\(=4500-\frac{125}{512}+6.288\)
\(=\left(4500+1728\right)-\frac{125}{512}\)
\(=6228-\frac{125}{512}\)
\(=...........\)

15^3+5.15^2-5^3 / 18^3+6.18^2-6^3
=3375+5.225-125 /5832+6.324-216
=3375+1125-125 /5832+1944-216
=4500-125 /7826-216
=4375 /7610
=875 /1522
mk ko bt viết phần nên viết phần bằng dấu gạch / nhé.mk cx ko bt đúng hay sai đâu nhé

A= \(\frac{25^3.5^3}{6.5^{10}}\)= \(\frac{\left(5^2\right)^3.5^3}{6.5^{10}}\)= \(\frac{5^6.5^3}{6.5^{10}}\)= \(\frac{5^9}{6.5^{10}}\)= \(\frac{5}{6}\)
B = \(\frac{2^5.6^3}{8^2.9^2}\)= \(\frac{2^5.\left(2.3\right)^3}{\left(2^3\right)^2.\left(3^2\right)^2}\)=\(\frac{2^5.2^3.3^3}{2^6.3^4}\)= \(\frac{2^8.3^3}{2^6.3^4}\)= \(\frac{2^2}{3}\)= \(\frac{4}{3}\)
C = \(\frac{15^3+5.15^2-5^3}{18^3+6.18^2-6^3}\)= \(\frac{5^3.3^3+5.5^2.3^2-5^3}{6^3.3^3+6.6^2.3^2-6^3}\)= \(\frac{5^3+5^3.3^2-5^3}{6^3.3^3+6^3.3^2-6^3}\)= \(\frac{5^3.\left(1+3^2-1\right)}{6^3.\left(3^3+3^2-1\right)}\)= \(\frac{5^3.9}{6^3.35}\)
=\(\frac{5^3.3^2}{2^3.3^3.7.5}\)
= \(\frac{25}{168}\)
D = \(\frac{\left(7^4-7^3\right)^2}{49^3}\)= \(\frac{[7^3\left(7-1\right)]^2}{\left(7^2\right)^3}\)= \(\frac{7^6.6^2}{7^6}\)= \(36\)


Gọi giá trị trên là : A
\(A=3^{100}-3^{99}+3^{98}+....+3^2-3+1\)
\(\Rightarrow3A=3^{101}-3^{100}+3^{99}-3^{98}+......+3^3-3^2+3\)
\(\Rightarrow3A+A=3^{101}+1\)
\(\Rightarrow4A=3^{101}+1\Rightarrow A=\frac{3^{101}+1}{4}\)
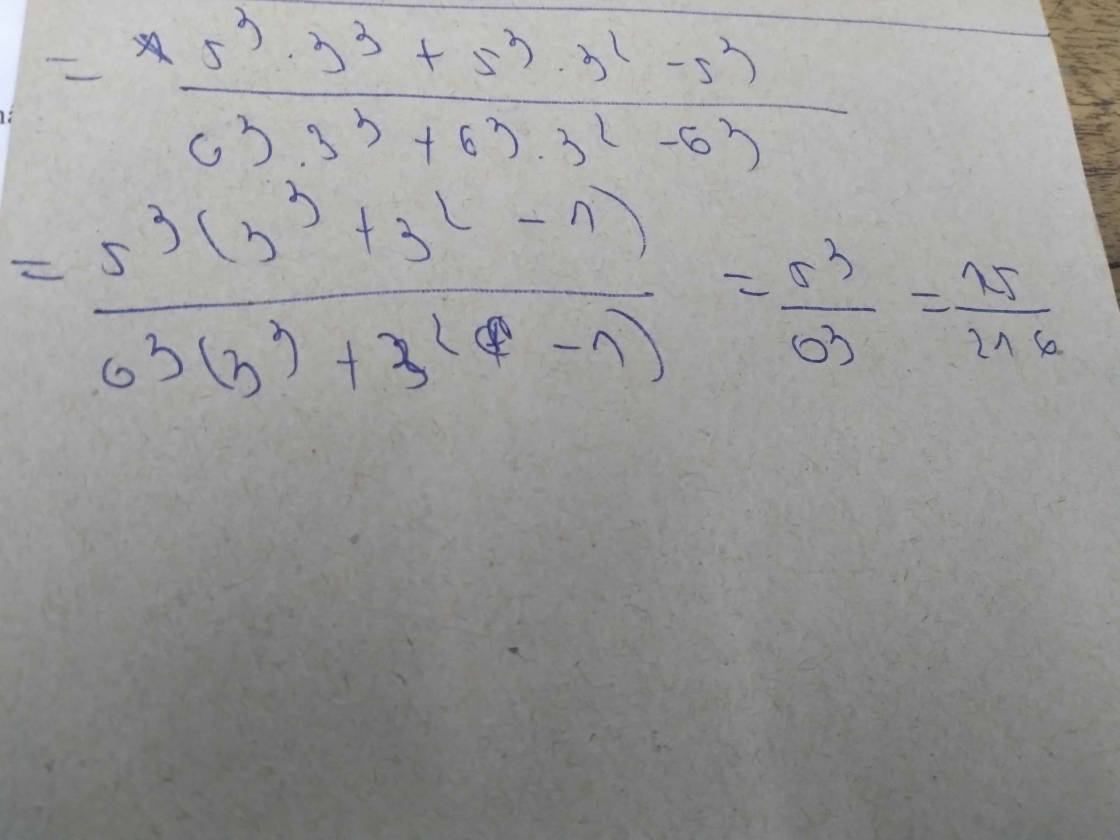
\(\dfrac{15^3+5.15^2-5^3}{18^3+6.18^2-6^3}\)
= \(\dfrac{\left(5.3\right)^3+5.\left(5.3\right)^2-5^3}{\left(6.3\right)^3+6.\left(6.3\right)^2-6^3}\)
= \(\dfrac{5^3.3^3+5^3.3^2-5^3}{6^3.3^3+6^3.3^2-6^3}\)
= \(\dfrac{5^3.\left(3^3+3^2-1\right)}{6^3.\left(3^3+3^2-1\right)}\)
=\(\dfrac{5^3}{6^3}=\dfrac{125}{216}\)