
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left\{{}\begin{matrix}2x^3+x^2y=3\left(1\right)\\2y^3+xy^2=3\end{matrix}\right.\)
Trừ vế theo vế hai phương trình ta được:
\(2\left(x^3-y^3\right)+\left(x^2y-xy^2\right)=0\)
\(\Leftrightarrow2\left(x-y\right)\left(x^2+xy+y^2\right)+xy\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(2x^2+3xy+2y^2\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left[2\left(x+\dfrac{9}{16}y\right)^2+\dfrac{7}{8}y^2\right]=0\left(2\right)\)
Do \(2\left(x+\dfrac{9}{16}y\right)^2+\dfrac{7}{8}y^2\ge0\), đẳng thức xảy ra khi \(x=y=0\)
Thay vào phương trình ta thấy \(x=y=0\) không phải là nghiệm
\(\Rightarrow2\left(x+\dfrac{9}{16}y\right)^2+\dfrac{7}{8}y^2>0\)
Khi đó \(\left(2\right)\Leftrightarrow x=y\)
\(\left(1\right)\Leftrightarrow2x^3+x^3=3\Leftrightarrow x=y=1\)
\(\Rightarrow x_0^3+y_0^3=2\)

Điều kiện xác định: x ≠ 0 .
Đặt t = x + 1 x ⇒ t 2 − 2 = x 2 + 1 x 2 ≥ 2 ⇒ t ≥ 2 ⇔ t ≥ 2 t ≤ − 2
Phương trình đã cho trở thành 2 t 2 − 2 − 3 t − 2 m + 1 = 0
⇔ 2 t 2 − 3 t − 2 m − 3 = 0 ⇔ 2 t 2 − 3 t − 3 = 2 m ( 1 )
Xét hàm số y = f ( t ) = 2 t 2 − 3 t − 3 có bảng biến thiên:

(1) Có nghiệm t thỏa mãn
t
≥
2
t
≤
−
2
k
h
i
2
m
≥
−
1
2
m
≥
11
⇔
m
≥
−
1
2
⇒
S
=
−
1
2
;
+
∞
Vậy T = 3
Đáp án cần chọn là: D

Đặt x + 1 t = t , t ≥ 2 khi đó phương trình trở thành 2 t 2 − 3 t − 5 m − 3 = 0 ( * )
Phương trình 2 x 2 + 1 x 2 - 3 x + 1 x - 5 m + 1 = 0 có nghiệm khi và chỉ khi phương trình (*) có nghiệm t thỏa mãn t ≥ 2
Số nghiệm của phương trình (*) bằng số giao điểm của parabol (P): y = 2 t 2 − 3 t − 3 và đường thẳng d : y = 5 m
Xét parabol P : y = 2 t 2 - 3 t - 3 ta có bảng biến thiên như sau:
Từ bảng biến thiên ta có phương trình (*) có nghiệm t ∈ ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ ) khi và chỉ khi 5 m ≥ - 1 hoặc 5 m ≥ 11
![]()
Vậy khi m ∈ − 1 5 ; + ∞ thì phương trình có nghiệm ⇒ a = 1 b = 5 ⇒ T = 5
Đáp án cần chọn là: B

3x4 + 2x2 – 1 = 0 (2)
Tập xác định : D = R.
Đặt t = x2, điều kiện t ≥ 0
Khi đó phương trình (2) trở thành :
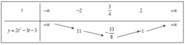
3t2 + 2t – 1 = 0 ⇔ (3t – 1)(t + 1) = 0
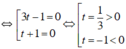
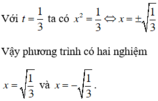
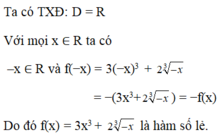
B= 1.2+2.3+3.4+...+2009.2010
=>3B=1.2.3+2.3.3+3.4.3+...+2009.2010.3
=1.2.(3-0)+2.3.(4-1)+3.4.(5-2)+...+2009.2010.(2011-2008)
=1.2.3-0.1.2+2.3.4-1.2.3+3.4.5-2.3.4+....+2009.2010.2011-2008.2009.2010
=2009.2010.2011
=>B=\(\frac{2009.2010.2011}{3}=2706866330\)
ta có: 1x2+2x3+3x4+....+n(n+1)
=1x(1+1)+2x(2+1)+3x(3+1)+....n(n+1)
=(1^2+2^2+3^2+¡+n^2)+(1+2+3+....+n)
=n(n+1)(2n+1)/6+n(n+1)/2
=[n(n+1)[(2n+1)+3]/6
thay n=2009=> B=\(\frac{2009.\left(2009+1\right).\left(2009.2+1\right)+3}{6}\)=2704847286