K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 9 2021
\(\Leftrightarrow\left(x^2-6xy+9y^2\right)+\left(x^2+6x+9\right)+\left(z^2-8z+16\right)=0\)
\(\Leftrightarrow\left(x-3y\right)^2+\left(x+3\right)^2+\left(z-4\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3y=0\\x+3=0\\z-4=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-1\\z=4\end{matrix}\right.\)
VQ
1
H9
HT.Phong (9A5)
CTVHS
24 tháng 10 2023
\(2x^2+y^2-2xy-8x+16=0\)
\(\Leftrightarrow\left(x^2-8x+16\right)+\left(x^2-2xy+y^2\right)=0\)
\(\Leftrightarrow\left(x-4\right)^2+\left(x-y\right)^2=0\)
Do: \(\left\{{}\begin{matrix}\left(x-4\right)^2\ge0\\\left(x-y\right)^2\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left(x-4\right)^2+\left(x-y\right)^2\ge0\)
Mặt khác: \(\left(x-4\right)^2+\left(x-y\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-4=0\\x-y=0\end{matrix}\right.\)
\(\Leftrightarrow x=y=4\)
Vậy: ...
12 tháng 9 2021
\(x^2+2y^2+2xy-14y+49=0\)
\(\Leftrightarrow\left(x+y\right)^2+\left(y-7\right)^2=0\)
Dấu '=' xảy ra khi y=7 và x=-7
DT
1
26 tháng 2 2018
\(2xy-6=4x-y\Leftrightarrow2xy-4x+y-2=4\)
\(\Leftrightarrow2x\left(y-2\right)+\left(y-2\right)=4\Leftrightarrow\left(y-2\right)\left(2x+1\right)=4\)(1)
Có \(x,y\inℤ\Rightarrow\hept{\begin{cases}2x+1\inℤ\\y-2\inℤ\end{cases}}\)
Từ (1) => 2x + 1 thuộc Ư(4) ; y - 2 thuộc Ư(4)
+) \(\hept{\begin{cases}2x+1=1\\y-2=4\end{cases}}\) +) \(\hept{\begin{cases}2x+1=2\\y-x=2\end{cases}}\)
+) \(\hept{\begin{cases}2x+1=4\\y-2=1\end{cases}}\) +) \(\hept{\begin{cases}2x+1=-2\\y-2=-2\end{cases}}\)
+) \(\hept{\begin{cases}2x+1=-1\\y-2=-4\end{cases}}\) +) \(\hept{\begin{cases}2x+1=-4\\y-2=-1\end{cases}}\)
Còn lại rất dễ bạn tự làm tiếp nhé
Chú ý điều kiện x ; y nguyên nhé !!!!
Tích cho mk nhoa !!!!! ~~
NV
0
TM
3
8 tháng 3 2016
Ở câu 2 viết 43/30 dưới dạng liên phân số rồi đối chiếu kết quả để tìm x,y,z( vì mỗi phân số chỉ viết dược dưới dạng 1 liên phân số
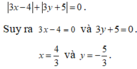
\(\Leftrightarrow\left(x^2+2xy+y^2\right)+4\left(x+y\right)+4+\left(x^2-12x+36\right)=0\)
\(\Leftrightarrow\left(x+y\right)^2+4\left(x+y\right)+4+\left(x-6\right)^2=0\)
\(\Leftrightarrow\left(x+y+2\right)^2+\left(x-6\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-6=0\\x+y+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=-8\end{matrix}\right.\)
\(y^2+2xy-12x+4\left(x+y\right)+2x^2+40=0\\ \Leftrightarrow\left[\left(x^2+2xy+y^2\right)+4\left(x+y\right)+4\right]+\left(x^2-12x+36\right)=0\\ \Leftrightarrow\left(x+y+2\right)^2+\left(x-6\right)^2=0\)
Vì \(\left\{{}\begin{matrix}\left(x+y+2\right)^2\ge0\forall x,y\\\left(x-6\right)^2\ge0\forall x\end{matrix}\right.\)
Nên \(\left(x+y+2\right)^2+\left(x-6\right)^2\ge0\forall x,y\)
Dấu"=" xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}x+y+2=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-8\\x=6\end{matrix}\right.\)
Vậy x = 6 và y = -8