Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(\sqrt{17}>\sqrt{16}\) , \(\sqrt{26}>\sqrt{25}\)
=>\(\sqrt{17}+\sqrt{26}+1>\sqrt{16}+\sqrt{25}+1=4+5+1=10\)
mà \(\sqrt{99}< \sqrt{100}=10\)
=> a > b

\(a)\) Ta có : \(A=\frac{\sqrt{x}+1}{\sqrt{x}-1}=\frac{\sqrt{x}-1+2}{\sqrt{x}-1}=\frac{\sqrt{x}-1}{\sqrt{x}-1}+\frac{2}{\sqrt{x}-1}=1+\frac{2}{\sqrt{x}-1}\)
Thay \(x=\frac{16}{9}\) vào \(A=1+\frac{2}{\sqrt{x}-1}\) ta được :
\(A=1+\frac{2}{\sqrt{\frac{16}{9}}-1}=1+\frac{2}{\sqrt{\left(\frac{4}{3}\right)^2}-1}=1+\frac{2}{\frac{4}{3}-1}=1+\frac{2}{\frac{1}{3}}=1+6=7\)
Vậy giá trị của \(A=7\) khi \(x=\frac{16}{9}\)
Thay \(x=\frac{25}{9}\) vào \(A=1+\frac{2}{\sqrt{x}-1}\) ta được :
\(A=1+\frac{2}{\sqrt{\frac{25}{9}}-1}=1+\frac{2}{\sqrt{\left(\frac{5}{3}\right)^2}-1}=1+\frac{2}{\frac{5}{3}-1}=1+\frac{2}{\frac{2}{3}}=1+3=4\)
Vậy giá trị của \(A=4\) khi \(x=\frac{25}{9}\)
\(b)\) Để \(A=5\) thì \(1+\frac{2}{\sqrt{x}-1}=5\)
\(\Rightarrow\)\(\frac{2}{\sqrt{x}-1}=4\)
\(\Rightarrow\)\(\frac{1}{\sqrt{x}-1}=\frac{1}{2}\)
\(\Rightarrow\)\(\sqrt{x}-1=2\)
\(\Rightarrow\)\(\sqrt{x}=3\)
\(\Rightarrow\)\(x=3^2\)
\(\Rightarrow\)\(x=9\)
Vậy để \(A=5\) thì \(x=9\)
\(c)\) Để \(A\inℤ\) thì \(1+\frac{2}{\sqrt{x}-1}\inℤ\)
\(\Rightarrow\)\(2⋮\left(\sqrt{x}-1\right)\)
\(\Rightarrow\)\(\left(\sqrt{x}-1\right)\inƯ\left(2\right)\)
Mà \(Ư\left(2\right)=\left\{1;-1;2;-2\right\}\)
Suy ra :
| \(\sqrt{x}-1\) | \(1\) | \(-1\) | \(2\) | \(-2\) |
| \(x\) | \(4\) | \(0\) | \(9\) | \(1\) |
Vậy để \(A\inℤ\) thì \(x\in\left\{0;1;4;9\right\}\)
Chúc bạn học tốt ~


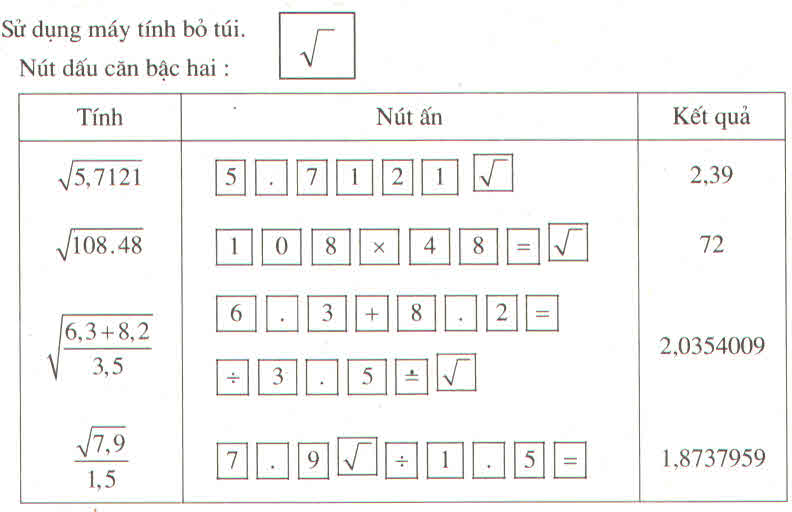
Chú ý: Trong các kết quả trên, hai kết quả đầu là căn bậc hai đúng, hai kết quả cuối là căn bậc hai gần đúng chính xác đến 6 chữ số thập phân (được làm tròn đến chữ số thập phân thứ sáu)

a, => 2^x = (2^3)^4/(2^4)^3 = 2^12/2^12 = 1 = 2^0
=> x = 0
c, => 4^x = 4^10.(4-3) = 4^10
=> x=10
d, => 2^2.3^x-1 + 2.3^x.9 = 2^2.3^6+2.3^9
=> 2.3^x-1 . (2+3.9) = 2.3^6.(2+3^3)
=> 2.3^x-1 . 27 = 2.3^6 . 27
=> 3^x-1 = 3^6
=> x-1 = 6
=> x = 7
e, => 2^x.(1/3+1/6+2) = 2^11.(2+1/2)
=> 2^x. 5/2 = 2^11. 5/2
=> 2^x = 2^11
=> x = 11
Tk mk nha
\(X+\sqrt{25}=10\)
\(X+5=10\)
\(X=10-5\)
\(X=5\)