Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bai nay ap dung tinh chat day ti so = nhau

Với các bài khá nâng cao như vậy bạn đăng tách ra nhé!
Answer:
a) Ta có: \(x:y:z=3:4:5\Rightarrow\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\)
Ta đặt: \(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=k\left(k\inℕ^∗\right)\)
\(\Rightarrow\hept{\begin{cases}x=3k\\y=4k\\z=5k\end{cases}}\)
Ta có: \(5z^2-3x^2-2y^2=594\)
\(\Rightarrow5.\left(5k\right)^2-3.\left(3k\right)^2-2.\left(4k\right)^2=594\)
\(\Rightarrow5.5^2k^2-3.3^2k^2-2.4^2k^2=594\)
\(\Rightarrow5.25k^2-3.9k^2-2.16.k^2=594\)
\(\Rightarrow125k^2-27k^2-32k^2=594\)
\(\Rightarrow k^2.\left(125-27-32\right)=594\)
\(\Rightarrow k^2.66=594\)
\(\Rightarrow k^2=9\)
\(\Rightarrow k=\pm3\)
Với \(k=3\Rightarrow\hept{\begin{cases}x=3.3=9\\y=3.4=12\\z=3.5=15\end{cases}}\)
Với \(k=-3\Rightarrow\hept{\begin{cases}x=\left(-3\right).3=-9\\y=\left(-4\right).3=-12\\z=\left(-5\right).3=-15\end{cases}}\)
Answer:
b) \(3.\left(x-1\right)=2.\left(y-2\right)\Rightarrow6.\left(x-1\right)=4.\left(y-2\right)\)
Mà: \(4.\left(y-2\right)=3.\left(z-3\right)\)
\(\Rightarrow6.\left(x-1\right)=4.\left(y-2\right)=3.\left(z-3\right)\)
\(\Rightarrow\frac{6.\left(x-1\right)}{12}=\frac{4.\left(y-2\right)}{12}=\frac{3.\left(z-3\right)}{12}\Rightarrow\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}=\frac{2x-2}{4}=\frac{3y-6}{9}==\frac{\left(2x-2\right)+\left(3y-6\right)-z}{4+9-4}=\frac{2x-2+3y-6-z}{9}=\frac{\left(2x+3y-z\right)-\left(2+6\right)}{9}=\frac{50-8}{9}=\frac{14}{3}\)
\(\Rightarrow\hept{\begin{cases}x-1=2.\frac{14}{3}=\frac{28}{3}\\y-2=3.\frac{14}{3}=14\\z-3=4.\frac{14}{3}=\frac{56}{3}\end{cases}}\Rightarrow\hept{\begin{cases}x=\frac{31}{3}\\y=16\\z=\frac{68}{3}\end{cases}}\)
c) \(\frac{2x}{3}=\frac{3y}{4}=\frac{4z}{5}\Rightarrow\frac{2x}{3.12}=\frac{3y}{4.12}=\frac{4z}{5.12}\Rightarrow\frac{x}{18}=\frac{y}{16}=\frac{z}{15}\)
Áp dụng tính chất của dãy tỉ số bằng nhau
\(\frac{x}{18}=\frac{y}{16}=\frac{z}{15}=\frac{x+y-z}{18+16-15}=\frac{38}{19}=2\)
\(\Rightarrow\frac{x}{18}=2\Rightarrow x=18.2=36\)
\(\Rightarrow\frac{y}{16}=2\Rightarrow y=16.2=32\)
\(\Rightarrow\frac{z}{15}=2\Rightarrow z=15.2=30\)

Miu Ti làm vớ vẩn
a)Từ \(x:y:z=3:4:5\Rightarrow\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\)
\(\Rightarrow\frac{3x^2}{27}=\frac{2y^2}{32}=\frac{5z^2}{125}\)
Theo t/c dãy tỉ số=nhau:
\(\frac{3x^2}{27}=\frac{2y^2}{32}=\frac{5z^2}{125}=\frac{5z^2-3x^2-2y^2}{125-27-32}=\frac{594}{66}=9\)
\(\)\(\Rightarrow3x^2=9.27=243\Rightarrow x^2=\frac{243}{3}=81\Rightarrow x\in\left\{9;-9\right\}\)
\(2y^2=9.32=288\Rightarrow y^2=\frac{288}{2}=144\Rightarrow y\in\left\{12;-12\right\}\)
\(5z^2=9.125=1125\Rightarrow z^2=\frac{1125}{5}=225\Rightarrow z\in\left\{15;-15\right\}\)
Vậy..............
b)Từ \(x+y=3\left(x-y\right)\Rightarrow3x-3y=x+y\Rightarrow3x-x=y+3y\Rightarrow2x=4y\)
\(\Rightarrow2x=2.2y\Rightarrow x=2y\Rightarrow\frac{x}{y}=2\)
Mà \(x+y=\frac{x}{y}\) (theo đề)
\(\Rightarrow x+y=2\Rightarrow2y+y=2\Rightarrow3y=2\Rightarrow y=\frac{2}{3}\)
khi đó \(x=2y=2.\frac{2}{3}=\frac{4}{3}\)
Vậy x=4/3;y=2/3
a/ Ta có x:y:z=3:4:5
=> \(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{5\cdot z^2-3\cdot x^2-2\cdot y^2}{5\cdot5^2-3.3^2-2\cdot4^2}=\frac{594}{66}=9\)
=> x=9.3=27
y=9*4=36
z=9*5=45
b/ Từ từ rồi tui làm

a) 3x = 2y \(\Rightarrow\)\(\frac{x}{2}=\frac{y}{3}\)\(\Rightarrow\frac{x}{2}.\frac{1}{5}=\frac{y}{3}.\frac{1}{5}\)\(\Rightarrow\frac{x}{10}=\frac{y}{15}\)
\(7y=5z\Rightarrow\frac{y}{5}=\frac{z}{7}\Rightarrow\frac{y}{5}.\frac{1}{3}=\frac{z}{7}.\frac{1}{3}\Rightarrow\frac{y}{15}=\frac{z}{15}\)
\(\Rightarrow\frac{x}{10}=\frac{y}{15}=\frac{z}{21}\Rightarrow\frac{x+y+z}{10+15+21}=\frac{32}{46}=\frac{2}{3}\)
\(\hept{\begin{cases}x=10.\frac{2}{3}=\frac{20}{3}\\y=15.\frac{2}{3}=10\\z=21.\frac{2}{3}=14\end{cases}}\)
Vậy \(\hept{\begin{cases}x=10.\frac{2}{3}=\frac{20}{3}\\y=15.\frac{2}{3}=10\\z=21.\frac{2}{3}=14\end{cases}}\)
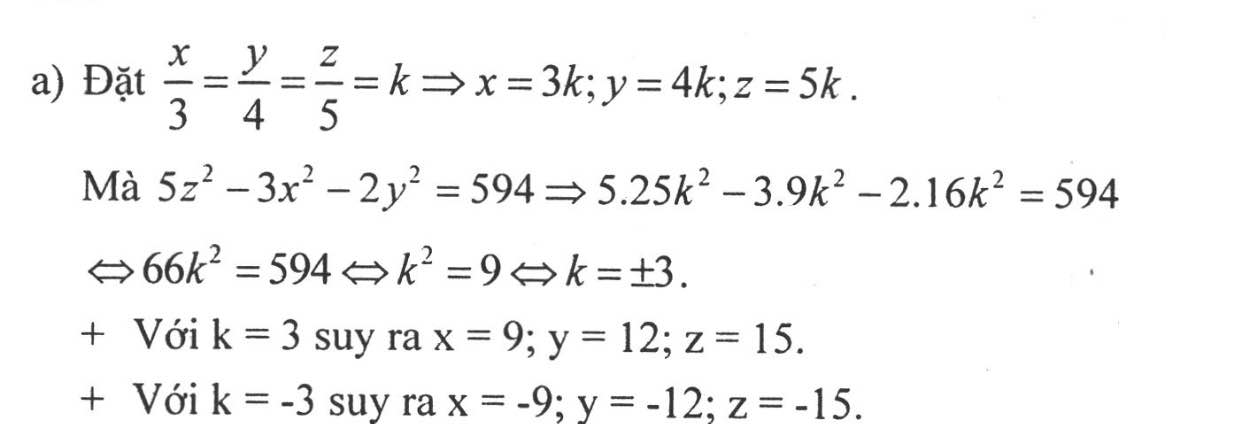
a) Ta có :
\(5z^2-3x^2-2y^2=594\)
\(x:y:z=3:4:5\)
\(\Leftrightarrow\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)
\(\Leftrightarrow\dfrac{3x^2}{27}=\dfrac{2y^2}{32}=\dfrac{5z^2}{125}\)
Aps dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{3x^2}{27}=\dfrac{2y^2}{32}=\dfrac{5z^2}{125}=\dfrac{5z^2-3x^2-2y^2}{125-27-32}=\dfrac{594}{66}=9\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3x^2}{27}=9\Leftrightarrow x^2=81\Leftrightarrow x\in\left\{9;-9\right\}\\\dfrac{2y^2}{32}=9\Leftrightarrow y^2=288\Leftrightarrow y\in\left\{12;-12\right\}\\\dfrac{5z^2}{125}=9\Leftrightarrow z^2=225\Leftrightarrow z\in\left\{15;-15\right\}\end{matrix}\right.\)
Vậy ..............
. Nốt câu b theo đề cậu đã sửa nhé.
\(x+y=x:y=3.\left(x-y\right)\)
\(\Rightarrow x+y=3x-3y\)
\(\Rightarrow y+3y=3x-x\)
\(\Rightarrow4y=2x\)
\(\Rightarrow2y=x\)
\(\Rightarrow x:y=2\)
\(\Rightarrow x+y=2y+y=2\)
\(\Rightarrow3y=2\)
\(\Rightarrow y=\dfrac{2}{3}\)
\(\Rightarrow x=\dfrac{4}{3}\)
Vậy \(x=\dfrac{4}{3}\) , \(y=\dfrac{2}{3}\) .