Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có \(x+y\le5=>-\left(x+y\right)\ge-5\)
có \(A=x+y+\dfrac{8}{x}+\dfrac{18}{y}=-\left(x+y\right)+2x+2y+\dfrac{8}{x}+\dfrac{18}{y}\)
có \(-\left(x+y\right)+2x+2y+\dfrac{8}{x}+\dfrac{18}{y}\ge-5+8+12=15\)
=>A\(\ge15\) dấu= xảy ra <=>x=2,y=3
vậy min A=15

\(b,\hept{\begin{cases}4\left(x+y\right)=5\left(x-y\right)\\\frac{40}{x+y}+\frac{40}{x-y}=9\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}4\left(x+y\right)^2\left(x-y\right)-5\left(x-y\right)^2\left(x+y\right)=0\\40\left(x-y\right)+40\left(x+y\right)-9\left(x-y\right)\left(x+y\right)=0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\left(x^2-y^2\right)\left[4\left(x+y\right)-5\left(x-y\right)\right]=0\\80x-9\left(x^2-y^2\right)=0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\left(x+y\right)\left(x-y\right)\left(9y-x\right)=0\\9\left(\frac{80}{9}x-x^2+y^2\right)=0\end{cases}}\)
\(\Rightarrow.......\)

a) Ta có: \(\left\{{}\begin{matrix}\dfrac{5}{x-1}+\dfrac{1}{y-1}=10\\\dfrac{1}{x-1}-\dfrac{3}{y-1}=18\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{x-1}+\dfrac{1}{y-1}=10\\\dfrac{5}{x-1}-\dfrac{15}{y-1}=90\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{16}{y-1}=-80\\\dfrac{1}{x-1}-\dfrac{3}{y-1}=18\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y-1=\dfrac{-1}{5}\\\dfrac{1}{x-1}=18+\dfrac{3}{y-1}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{4}{5}\\x-1=\dfrac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{4}{3}\\y=\dfrac{4}{5}\end{matrix}\right.\)

a: \(\sqrt{\dfrac{3}{20}}=\sqrt{\dfrac{15}{100}}=\dfrac{\sqrt{15}}{10}\)
b: \(\sqrt{\dfrac{5}{18}}=\sqrt{\dfrac{10}{36}}=\dfrac{\sqrt{10}}{6}\)
c: \(ab\sqrt{\dfrac{a}{b}}=ab\cdot\dfrac{\sqrt{a}}{\sqrt{b}}=a\sqrt{ab}\)
d: \(\dfrac{x}{y}\sqrt{\dfrac{y}{x}}=\dfrac{x}{y}\cdot\dfrac{\sqrt{y}}{\sqrt{x}}=\sqrt{\dfrac{x}{y}}=\dfrac{\sqrt{xy}}{y}\)

\(1=2\left(\dfrac{9}{x}+\dfrac{1}{y}\right)\ge2.\dfrac{\left(3+1\right)^2}{x+y}=\dfrac{32}{x+y}\)
\(\Rightarrow x+y\ge32\)
\(A_{min}=32\) khi \(\left(x;y\right)=\left(24;8\right)\)

Ta có:
x + x + x = 30 =>x = 30 : 3 = 10
y + y - x = 2.Ta đã biết x = 10 nên y + y = 2 + 10 =12 =>y =12 : 2 =6
z + z + y =18.Ta đã biết y=6 nên z+z=18-6=12 =>z=12 : 2 = 6
Vậy x +y + z =10+6+6=22
\(x+x+x=30\Leftrightarrow x=30:3=10\)
\(y+y-x=2\)Vì \(x=10\)=> \(y=12:2=6\)
\(z+z+y=18\)Vì y = 6 =>Z + Z =18 -6 = 12
\(\Leftrightarrow y=12:2=6\)
\(x+y+z=10+6+6=22\)
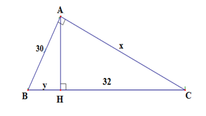
Ta có: BC = BH + HC = y + 32
Áp dụng hệ thức lượng A B 2 = B H . B C trong tam giác vuông ABC ta có:
⇔ y − 18 = 0 y + 50 = 0 ⇔ y = 18 N y = − 50 L
Suy ra y = 18 => BC = 18 + 32 = 50
Áp dụng hệ thức lượng A C 2 = C H . B C ta có:
Vậy c = 40; y = 18
Đáp án cần chọn là: D