K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
N
0
5 tháng 8 2019
\(3x=5y\Rightarrow\frac{x}{5}=\frac{y}{3}\)
ÁP DỤNG DÃY TỈ SỐ BẰNG NHAU TA CÓ
\(\frac{x}{5}=\frac{y}{3}=\frac{xy}{15}=\frac{135}{15}=9\)
\(\Rightarrow\hept{\begin{cases}x=45\\y=27\end{cases}}\)
D
1
27 tháng 8 2019
Ta có \(\frac{3x}{4}=\frac{5y}{6}=\frac{6z}{11}\)
=> \(\frac{x}{\frac{4}{3}}=\frac{y}{\frac{6}{5}}=\frac{z}{\frac{11}{6}}\)
Áp dụng t/c dãy tỉ số bằng nhau ta có :
\(\frac{x}{\frac{4}{3}}=\frac{y}{\frac{6}{5}}=\frac{z}{\frac{11}{6}}=\frac{x+y+z}{\frac{4}{3}+\frac{6}{5}+\frac{11}{6}}=\frac{-262}{\frac{131}{30}}=-60\)
Đến đây tìm được x,y,z
3 tháng 10 2021
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{-5}=\dfrac{-3x+2y}{-12-10}=\dfrac{55}{-22}=\dfrac{-5}{2}\)
Do đó: \(\left\{{}\begin{matrix}x=\dfrac{-20}{2}=-10\\y=\dfrac{25}{2}\end{matrix}\right.\)
b: Ta có: \(\dfrac{x}{y}=\dfrac{-7}{4}\)
nên \(\dfrac{x}{-7}=\dfrac{y}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{-7}=\dfrac{y}{4}=\dfrac{4x-5y}{-28-20}=\dfrac{72}{-48}=\dfrac{-3}{2}\)
Do đó: \(\left\{{}\begin{matrix}x=\dfrac{21}{2}\\y=\dfrac{-12}{2}=-6\end{matrix}\right.\)
PT
1
CM
18 tháng 11 2019
Đặt x2 = a (a ≥ 0), y2 = b (b ≥ 0)
Ta có: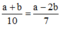 
và a2b2 = 81.
Theo tính chất của dãy tỉ số bằng nhau ta có:
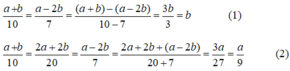
Từ (1) và (2) suy ra a/9 = b ⇒ a = 9b
Do a2b2 = 81 nên (9b)2.b2 = 81 ⇒ 81b4 = 81 ⇒ b4 = 1 ⇒ b = 1 (vì b ≥ 0)
Suy ra a = 9. 1 = 9
Ta có x2 = 9 và y2 = 1. Suy ra x = 3 hoặc x = -3, y = 1 hoặc y = -1.
PT
2
KT
19 tháng 7 2018
\(2x=3y\)\(\Rightarrow\)\(\frac{x}{3}=\frac{y}{2}\)hay \(\frac{x}{6}=\frac{y}{4}\)
\(5y=4z\)\(\Rightarrow\)\(\frac{y}{4}=\frac{z}{5}\)
suy ra: \(\frac{x}{6}=\frac{y}{4}=\frac{z}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{6}=\frac{y}{4}=\frac{z}{5}=\frac{x-y}{6-4}=\frac{57}{2}\)
đến đây bạn làm tiếp nhé
19 tháng 7 2018
ta có: \(2x=3y\Rightarrow\frac{x}{3}=\frac{y}{2}\Rightarrow\frac{x}{6}=\frac{y}{4}\)
\(5y=4z\Rightarrow\frac{y}{4}=\frac{z}{5}\)
\(\Rightarrow\frac{x}{6}=\frac{y}{4}=\frac{z}{5}\)
ADTCDTSBN
có: \(\frac{x}{6}=\frac{y}{4}=\frac{x-y}{6-4}=\frac{57}{2}\)
=> x/6 = 57/2 => ...
...
z/5 = 57/2 => ...
bn tự tính ik nha!
31 tháng 8 2018
1) ta có: \(x:3=y.15\Rightarrow x\cdot\frac{1}{3}=y.15\Rightarrow\frac{x}{15}=\frac{y}{\frac{1}{3}}\)
ADTCDTSBN
...
2) bn ghi thiếu đề r
3) ta có: \(3x=7y\Rightarrow\frac{x}{7}=\frac{y}{3}=k\Rightarrow\hept{\begin{cases}x=7k\\y=3k\end{cases}}\)
mà xy = 189 => 7k.3k = 189
21 k2 = 189
k2 = 9 = 32 = (-3)2 => k = 3 hoặc k = - 3
TH1: k = 3
x = 7.3 => x = 21
y = 3.3 => y = 9
...
31 tháng 8 2018
4) ta có: \(4x=5y\Rightarrow\frac{x}{5}=\frac{y}{4}\Rightarrow\frac{x^2}{25}=\frac{y^2}{16}\)
ADTCDTSBN
...
DN
2
6 tháng 2 2020
ý bạn là \(1+\frac{5y}{24}\)hay là \(\frac{1+5y}{24}\)
Ta có : \(3x=5y\Rightarrow\frac{x}{5}=\frac{y}{3}\Leftrightarrow\left(\frac{x}{5}\right)^2=\left(\frac{y}{3}\right)^2\Leftrightarrow\frac{x^2}{25}=\frac{y^2}{9}\)
Áp dụng tính chất 2 phân số bằng nhau ta có :
\(\frac{x^2}{25}=\frac{y^2}{9}=\frac{x^2+y^2}{25+9}=\frac{136}{34}=4\)
\(\Rightarrow\frac{x^2}{25}=4\Rightarrow x^2=100\Rightarrow x=\pm10\)
\(\Rightarrow\frac{y^2}{9}=4\Rightarrow y^2=36\Rightarrow y=\pm6\)
Vì 3x = 2y nên x ;y phải cùng dấu
=> Các cặp (x;y) thỏa mãn là : (-10 ; - 6) ; (10 ; 6)
Vậy các cặp (x;y) thỏa mãn là : (-10 ; - 6) ; (10 ; 6)