Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Cách 1: Từ \(13x=7y\) suy ra \(\frac{x}{7}=\frac{y}{13}\). Theo tính chất của dãy các tỉ số bằng nhau ta có: \(\frac{x}{7}=\frac{y}{13}=\frac{x+y}{7+13}=\frac{40}{20}=2\).
Từ đó ta được: \(x=7.2=12;y=13.2=26\).
Cách 2: Đặt \(\frac{x}{7}=\frac{y}{13}=k\) ta có: \(x=7k,y=13k\).
Thay vào hệ thức \(x+y=40\) ta được \(7k+13k=40\), suy ra \(k=2.\)
Do đó \(x=7.2=14,y=13.2=26\)
b) Làm tương tự câu a) ta có:
\(\frac{x}{19}=\frac{y}{21}=\frac{x-y}{19-21}=\frac{4}{-2}=-2\)
Từ đó \(x=19.\left(-2\right)=-38,y=21.\left(-2\right)=-42\)

1) \(\Rightarrow\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x-y+z}{8-12+15}=\dfrac{10}{11}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{8}=\dfrac{10}{11}\\\dfrac{y}{12}=\dfrac{10}{11}\\\dfrac{z}{15}=\dfrac{10}{11}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{80}{11}\\y=\dfrac{120}{11}\\z=\dfrac{150}{11}\end{matrix}\right.\)
2) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=\dfrac{y}{4}\\\dfrac{y}{5}=\dfrac{z}{7}\end{matrix}\right.\) \(\Rightarrow\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}=\dfrac{2x}{30}=\dfrac{3y}{60}=\dfrac{2x+3y-z}{30+60-28}=\dfrac{136}{62}=\dfrac{68}{31}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{15}=\dfrac{68}{31}\\\dfrac{y}{20}=\dfrac{68}{31}\\\dfrac{z}{28}=\dfrac{68}{31}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1020}{31}\\y=\dfrac{1360}{31}\\z=\dfrac{1904}{31}\end{matrix}\right.\)
3) \(\Rightarrow\dfrac{3x-9}{15}=\dfrac{5y-25}{5}=\dfrac{7z+21}{49}\)
Áp dụng t/c dtsbn:
\(\dfrac{3x-9}{15}=\dfrac{5y-25}{5}=\dfrac{7z+21}{49}=\dfrac{3x+5y-7z-9-25-21}{15+5-49}=-\dfrac{45}{29}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{3x-9}{15}=-\dfrac{45}{29}\\\dfrac{5y-25}{5}=-\dfrac{45}{29}\\\dfrac{7z+21}{49}=-\dfrac{45}{29}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{138}{29}\\y=\dfrac{100}{29}\\z=-\dfrac{402}{29}\end{matrix}\right.\)

a, Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{3}=\frac{y}{-2}=\frac{2x+5y}{2.3+5.\left(-2\right)}=-\frac{12}{-4}=3\)
\(x=-3;y=6\)
b, Theo bài ra ta có : \(x:y=4:5\Leftrightarrow\frac{x}{4}=\frac{y}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{4}=\frac{y}{5}=\frac{x-y}{4-5}=\frac{13}{-1}=-13\)
\(x=-52;y=-65\)
c, Theo bài ra ta có: \(4x=7y\Leftrightarrow\frac{x}{7}=\frac{y}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{7}=\frac{y}{4}=\frac{x-y}{7-4}=\frac{12}{3}=4\)
\(x=28;y=16\)

a) Ta có: \(\dfrac{2x}{3}=\dfrac{3y}{4}=\dfrac{4z}{5}\)
nên \(\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}=\dfrac{x+y+z}{\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}}=\dfrac{49}{\dfrac{49}{12}}=12\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{2x}{3}=12\\\dfrac{3y}{4}=12\\\dfrac{4z}{5}=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=36\\3y=48\\4z=60\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=18\\y=16\\z=20\end{matrix}\right.\)
Vậy: (x,y,z)=(18;16;20)
b) Đặt \(\dfrac{x}{5}=\dfrac{y}{3}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=5k\\y=3k\end{matrix}\right.\)
Ta có: \(x^2-y^2=4\)
\(\Leftrightarrow\left(5k\right)^2-\left(3k\right)^2=4\)
\(\Leftrightarrow16k^2=4\)
\(\Leftrightarrow k\in\left\{\dfrac{1}{2};-\dfrac{1}{2}\right\}\)
Trường hợp 1: \(k=\dfrac{1}{2}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=5k=5\cdot\dfrac{1}{2}=\dfrac{5}{2}\\y=3k=3\cdot\dfrac{1}{2}=\dfrac{3}{2}\end{matrix}\right.\)
Trường hợp 2: \(k=-\dfrac{1}{2}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=5k=5\cdot\dfrac{-1}{2}=\dfrac{-5}{2}\\y=3k=3\cdot\dfrac{-1}{2}=\dfrac{-3}{2}\end{matrix}\right.\)
Vậy: \(\left(x,y\right)\in\left\{\left(\dfrac{5}{2};\dfrac{3}{2}\right);\left(-\dfrac{5}{2};-\dfrac{3}{2}\right)\right\}\)
a)
Theo tính chất của dãy tỉ số bằng nhau, ta có :
\(\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}=\dfrac{x+y+z}{\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}}=\dfrac{49}{\dfrac{49}{12}}=12\)
Suy ra :
\(x=\dfrac{12.3}{2}=18\\ y=\dfrac{12.4}{3}=16\\ z=\dfrac{12.5}{4}=15\)
b)
\(x=\dfrac{y}{3}.5=\dfrac{5y}{3}\\ x^2-y^2=4\\ \Leftrightarrow\left(\dfrac{5y}{3}\right)^2-y^2=4\\ \Leftrightarrow\dfrac{16y^2}{9}=4\Leftrightarrow y=\pm\dfrac{3}{2} \)
Với $y = \dfrac{3}{2}$ thì $x = \dfrac{5}{2}$
Với $y = \dfrac{-3}{2}$ thì $x = \dfrac{-5}{2}$
c)
\(\dfrac{x}{y+z+1}=\dfrac{y}{z+x+1}=\dfrac{z}{x+y-2}=\dfrac{x+y+z}{2x+2y+2z}=\dfrac{1}{2}\)
Suy ra :
\(2x=y+z+1\Leftrightarrow y+z=2x-1\)
Mặt khác :
\(x+y+z=\dfrac{1}{2}\Leftrightarrow x+2x-1=\dfrac{1}{2}\Leftrightarrow x=\dfrac{1}{2}\)
\(2y=x+z+1=z+\dfrac{3}{2}\)
Mà \(y+z=0\Leftrightarrow z=-y\)
nên suy ra: \(y=\dfrac{1}{2};z=-\dfrac{1}{2}\)

Ta co:
\(\frac{x}{y}=\frac{17}{3}\Rightarrow\frac{x}{3}=\frac{y}{17}=\frac{x+y}{3+17}=3\)
\(\frac{x}{3}=3\Rightarrow x=9\)
\(\frac{y}{17}=3\Rightarrow y=51\)
b)Ta co:
\(\frac{x}{19}=\frac{y}{21}\Rightarrow\frac{2x}{38}=\frac{y}{21}=\frac{2x-y}{38-21}=2\)
\(\frac{2x}{38}=2\Rightarrow x=38\)
\(\frac{y}{21}=2\Rightarrow y=42\)
Ta co:
\(\frac{x^2}{9}=\frac{y^2}{16}=\frac{x^2+y^2}{9+16}=4\)
\(\frac{x^2}{9}=4\Rightarrow x^2=36\Rightarrow x=6\)
\(\frac{y^2}{16}=4\Rightarrow y^2=64\Rightarrow y=8\)
g)\(3x=2y\Leftrightarrow\frac{x}{2}=\frac{y}{3}\)
\(7y=5z\Leftrightarrow\frac{y}{5}=\frac{z}{7}\)
\(\frac{x}{10}=\frac{y}{15};\frac{y}{15}=\frac{z}{21}\Rightarrow\frac{x}{10}=\frac{y}{15}=\frac{z}{21}=\frac{x-y+z}{10-15+21}=2\)
\(\frac{x}{10}=2\Rightarrow x=20;\frac{y}{15}=2\Rightarrow y=30;\frac{z}{21}=2\Rightarrow z=42\)

e, ta có \(2x=3y\Rightarrow\frac{x}{3}=\frac{y}{2}\Rightarrow\frac{x^2}{9}=\frac{y^2}{4}\)
AĐTCTSBN ta có \(\frac{x^2}{9}=\frac{y^2}{4}=\frac{x^2+y^2}{9+4}=\frac{52}{13}=4\)
\(\Rightarrow\hept{\begin{cases}x=2\cdot3=6\\y=2\cdot2=4\end{cases}}\)
a) Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{7}=\frac{y}{4}=\frac{x-y}{7-4}=\frac{30}{3}=10\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{7}=10\Leftrightarrow x=70\\\frac{y}{4}=10\Leftrightarrow y=40\end{cases}}\)
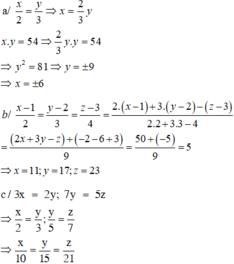
a, Thay \(x=\frac{7}{13}\)vào \(x+y=40\)=> \(\frac{7}{13}+y=40\Rightarrow y=40-\frac{7}{13}\Rightarrow y=\frac{513}{13}\)
b, Ta có: \(13x=7y\Rightarrow\frac{x}{7}=\frac{y}{13}\)và x+y=-60. Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{7}=\frac{y}{13}=\frac{x+y}{7+13}=\frac{-60}{20}=-3\) \(\Rightarrow\hept{\begin{cases}\frac{x}{7}=-3\Rightarrow x=-3\cdot7=-21\\\frac{y}{13}=-3\Rightarrow y=-3\cdot13=-39\end{cases}}\)