Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A) 4x^2 - 3x -7 = 4x^2 + 4x - 7x - 7
=(x +1)(4x - 7) =0
=>x+1=0 <=> x=-1
hoac 4x-7=0 <=> x=7/4
Nhu cau sau lam tuong tu

Giải:
a) \(3x\left(12x-4\right)-9x\left(4x-3\right)=30\)
\(\Leftrightarrow36x^2-12x-36x^2+27x=30\)
\(\Leftrightarrow-12x+27x=30\)
\(\Leftrightarrow15x=30\)
\(\Leftrightarrow x=2\)
Vậy ...
b) \(2x\left(x-1\right)+x\left(5-2x\right)=15\)
\(\Leftrightarrow2x^2-2x+5x-2x^2=15\)
\(\Leftrightarrow-2x+5x=15\)
\(\Leftrightarrow3x=15\)
\(\Leftrightarrow x=5\)
Vậy ...

a) Đặt f(x) =\(\left(2x^2-9\right)\left(-x^2+1\right)\)
Ta có: \(f\left(x\right)=0\Leftrightarrow\left(2x^2-9\right)\left(-x^2+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x^2-9=0\\-x^2+1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}2x^2=9\\-x^2=-1\end{cases}}}\)
\(\Leftrightarrow\orbr{\begin{cases}x^2=\frac{9}{2}\\x^2=1\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\pm\sqrt{\frac{9}{2}}\\x=\pm1\end{cases}}}\)
Vậy \(x\in\left\{\pm\sqrt{\frac{9}{2}};\pm1\right\}\)là nghiệm của đa thức f(x)

a) \(f\left(1\right)=5-2-3+4\)
\(=0\)
\(\Rightarrow f\left(1\right)⋮x-1\)
Vậy ...
a) \(f\left(-1\right)=5.\left(-1\right)^3-2.\left(-1\right)^2-3.\left(-1\right)+4\)
\(=-5-2+3+4\)
\(=0\)
Vậy x=-1 là nghiệm của đa thức f(x)
b) \(f\left(-1\right)=a.\left(-1\right)^3+b.\left(-1\right)^2+c.\left(-1\right)+d\)
\(=-a+b-c+d\)
\(=-\left(a-b+c-d\right)\)
\(=-\left[\left(a+c\right)-\left(b+d\right)\right]\)
\(=0\)( vì a+c=b+d nên (a+c) - (b+d) =0 )
Vậy x=-1 là nghiệm của đa thức f(x)

a ) \(A=\left|x+1\right|+\left|x+2\right|-2x+3\ge2x+3-2x+3=6\)
Dấu " = " xảy ra khi \(\left(x+2\right)\left(x+1\right)\ge0\)
b )
\(B=\left|2x+3\right|+\left|1-2x\right|\ge\left|2x+3+1-2x\right|=4\)
Dấu " = " xảy ra khi \(\left(2x+3\right)\left(1-2x\right)\ge0\)
c )
\(C=\left|x-1\right|+\left|x-2\right|+\left|x-2\right|\ge\left|x-1\right|+\left|2-x\right|\ge\left|x-1+2-x\right|=1\)
Dấu " = " xảy ra khi \(x=2\)

a) Ta có : 2x=3y ->x/3=y/2 =x/21=y/14 (1)
5y=7z ->y/7=z/5 = y/14=z/10 (2)
Từ (1) và (2) ->x/21=y/14=z/10
Ta lại có:x/21=3x/21*3=3x/63
y/14=7y/7*14=7y/98
z/10=5z/5*10=5z/50
-> 3x/63=7y/98=5z/50
Áp dụng tính chất của dãy tỉ số bằng nhau :
3x/63=7y/98=5z/50 -> 3x-7y+5z/63-98+50=30/15=2
->3x/63=2 ->x=42
-> 7y/98=2 ->y=28
-> 5z/50=2 ->z=20
Vậy x=42;y=28;z=20
( Mình không chắc lắm, vì tính lại nó ra đáp số khác bạn thử tính lại xem, nếu sai cho minh xin lỗi.)

a, 3 : ( 1 - 3/2x ) = 4 : ( 2 - x )
<=> \(\frac{3}{1-\frac{3}{2}x}=\frac{4}{2-x}\)
<=> 3 ( 2 - x ) = 4 ( 1 - 3/2x )
<=> 6 - 3x = 4 - 6x
<=> -3x + 6x = 4 - 6
<=> 3x = -2
<=> x = -2/3
b, 2.3x + 3x-1 = 7( 32 + 2.62 )
b, 2.3x + 3x-1 = 7( 32 + 2.62 )
<=> 2.3x + 3x-1 = 7.81
<=> 3x-1(2.3 + 1) = 7.81
<=> 3x-1.7 = 7.81
<=> 3x-1=81
<=> 3x-1 = 34
=> x - 1 = 4 => x = 5
a) bn xem lại xem đề bài có đúng k nhé !
Nếu đúng thì kq sẽ là 1
b)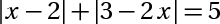
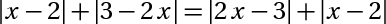
\(\Rightarrow x\in\begin{cases}0\\\frac{10}{3}\end{cases}\)
c)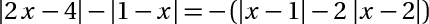
pải lập bảng xét dấu chứ bn