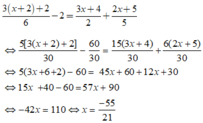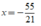Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có:
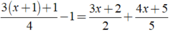
⇔ 15 x + 1 + 5 − 20 20 = 10 3 x + 2 + 4 4 x + 5 20
⇔ 15 x + 15 + 5 - 20 = 30 x + 20 + 16 x + 20 ⇔ 31 x = - 40 ⇔ x = - 40 / 31 .
Vậy phương trình đã cho có nghiệm là x = - 40/31.
Chọn đáp án A.

1/ \(M=x^2-2x.15+225-198\)
\(M=\left(x-15\right)^2-198\ge-198\)
\(Min\)\(M=-198\Leftrightarrow x=15\)


a) 5 - 4x = 3x - 9
\(\Leftrightarrow5-4x-3x+9=0\)
\(\Leftrightarrow14-7x=0\)
\(\Leftrightarrow7x=14\Leftrightarrow x=2\)
Vậy \(S=\left\{2\right\}\)
b) \(\left(x-4\right)\left(3x+9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\3x+9=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-3\end{matrix}\right.\)
Vậy \(S=\left\{-3;4\right\}\)
c) \(\dfrac{x}{x+4}+\dfrac{12}{x-4}=\dfrac{4x+48}{x\cdot x-16}\)(1)
ĐKXĐ: \(x\ne\pm4\)
\(\left(1\right)\Leftrightarrow\dfrac{x\left(x-4\right)+12\left(x+4\right)-4x-48}{\left(x+4\right)\left(x-4\right)}=0\)
\(\Leftrightarrow x^2-4x+12x+48-4x-48=0\)
\(\Leftrightarrow x^2+4x=0\)
\(\Leftrightarrow x\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(TM\right)\\x=-4\left(KTM\right)\end{matrix}\right.\)
Vậy \(S=\left\{0\right\}\)
d) \(4-2x=7-x\)
\(\Leftrightarrow4-2x-7+x=0\)
\(\Leftrightarrow-x-3=0\)
\(\Leftrightarrow-x=3\Leftrightarrow x=-3\)
Vậy \(S=\left\{-3\right\}\)
e) \(\left(x+4\right) \left(8-4x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\8-4x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=2\end{matrix}\right.\)
Vậy \(S=\left\{-4;2\right\}\)
f) \(\dfrac{x}{x+5}+\dfrac{11}{x-5}=\dfrac{x+55}{x\cdot x-25}\left(2\right)\)
ĐKXĐ: \(x\ne\pm5\)
\(\left(2\right)\Leftrightarrow\dfrac{x\left(x-5\right)+11\left(x+5\right)-x-55}{\left(x+5\right)\left(x-5\right)}=0\)
\(\Leftrightarrow x^2-5x+11x+55-x-55=0\)
\(\Leftrightarrow x^2+5x=0\)
\(\Leftrightarrow x\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(TM\right)\\x=-5\left(KTM\right)\end{matrix}\right.\)
Vậy \(S=\left\{0\right\}\)
g) \(\dfrac{3x+2}{2}-\dfrac{3x+1}{6}=\dfrac{5}{3}+2x\)
\(\Leftrightarrow\dfrac{3\left(3x+2\right)-3x-1-10-12x}{6}=0\)
\(\Leftrightarrow9x+6-3x-1-10-12x=0\)
\(\Leftrightarrow-6x-5=0\)
\(\Leftrightarrow-6x=5\)
\(\Leftrightarrow x=-\dfrac{5}{6}\)
Vậy \(S=\left\{-\dfrac{5}{6}\right\}\)
h) \(2x-\left(3-5x\right)=4\left(x+3\right)\)
\(\Leftrightarrow2x-3+5x-4x-12=0\)
\(\Leftrightarrow3x-15=0\)
\(\Leftrightarrow x=5\)
Vậy \(S=\left\{5\right\}\)
i) \(3x-6+x=9-x\)
\(\Leftrightarrow3x-6+x-9+x=0\)
\(\Leftrightarrow5x-15=0\)
\(\Leftrightarrow x=3\)
Vậy \(S=\left\{3\right\}\)
k)\(2t-3+5t=4t+12\)
\(\Leftrightarrow2t-3+5t-4t-12=0\)
\(\Leftrightarrow3t-15=0\)
\(\Leftrightarrow t=5\)
Vậy \(S=\left\{5\right\}\)

Cho hoi dap de hoi chi khong duoc noi lung tung day la pham loi trong hoi dap

Lời giải:
$x^{99}+x^{55}+x^n+x-7=(x^{99}+x)+(x^{55}+x)+x^n-x-7$
$=x(x^{98}+1)+x(x^{54}+1)+x^n-x-7$
Hiển nhiên: $x^{98}+1=(x^2)^{49}+1\vdots x^2+1$
$x^{54}+1=(x^2)^{27}+1\vdots x^2+1$
Xét các TH sau:
TH1: $n=4k$ thì $x^n-1=x^{4k}-1\vdots x^4-1\vdots x^2+1$. Khi đó đa thức dư là $-x-6$
TH2: $n=4k+1$ thì $x^{n}-x=x(x^{4k}-1)\vdots x^2+1$. Khi đó đa thức dư là $-7$
TH3: $n=4k+2$ thì: $x^n+1=x^{4k+2}+1=(x^2)^{2k+1}+1\vdots x^2+1$. Khi đó đa thức dư là $-x-8$
TH4: $n=4k+3$ thì $x^n+x=x^{4k+3}+x=x(x^{4k+2}+1)\vdots x^2+1$. Khi đó đa thức dư là $-2x-7$