
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đặt \(A=\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}+\frac{1}{256}\)
\(A=\frac{1}{2^3}+\frac{1}{2^4}+\frac{1}{2^5}+\frac{1}{2^6}+\frac{1}{2^7}+\frac{1}{2^8}\)
\(2A=\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+\frac{1}{2^5}+\frac{1}{2^6}+\frac{1}{2^7}\)
\(2A-A=\left(\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+\frac{1}{2^5}+\frac{1}{2^6}+\frac{1}{2^7}\right)-\left(\frac{1}{2^3}+\frac{1}{2^4}+\frac{1}{2^5}+\frac{1}{2^6}+\frac{1}{2^7}+\frac{1}{2^8}\right)\)
\(A=\frac{1}{2^2}-\frac{1}{2^8}\)
\(A=\frac{1}{4}-\frac{1}{256}=\frac{63}{256}\)
\(\Rightarrow\frac{63}{256}.x=\frac{1}{512}=\frac{1}{2^9}\)
\(\Rightarrow\frac{63}{2^8}.x=\frac{1}{2^9}\)
\(\Rightarrow x=\frac{1}{2^9}:\frac{63}{2^8}=\frac{1}{2^9}.\frac{2^8}{63}=\frac{1}{2.63}=\frac{1}{126}\)
Ủng hộ mk nha !!! ^_^

S=1/4+1/8+1/16+1/32+1/64+1/128
\(S=\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^7}\)
\(2S=2\left(\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^7}\right)\)
\(2S=\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^6}\)
\(2S-S=\left(\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^6}\right)-\left(\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^7}\right)\)
\(S=\frac{1}{2}-\frac{1}{2^7}\)
S=(1/2-1/4)+(1/4-1/8)+(1/8-1/16)+(1/16-1/32)+(1/32-1/64)+(1/64-1/128)
S=1/2-1/4+1/4-1/8+1/8-1/16+1/16-1/32+1/32-1/64+1/64-1/128
S=1/2-(1/4-1/4)+(1/8-1/8)+(1/16-1/16)+(1/32-1/32)+(1/64-1/64)-1/128
S=1/2-1/128
S=63/128

Đặt A=\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)
\(2A=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\)
\(2A-A=1-\frac{1}{128}\)
\(A=\frac{127}{128}\)
\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}=\frac{127}{128}\)


1/2+1/4+1/8+1/16+1/32+1/64+1/128
=64/128+32/128+16/128+8/126+4/126+2/126+1/128
=64+32+16+8+4+2+1/128
=123/128
C=1/2+1/4+1/8+1/16+1/32+1/64+1/128
C=1-1/2+1/2-1/4+1/4-1/8+1/8-1/16+1/16-1/32+1/32-1/64+1/64-1/128
C=1-1/128
C=127/128

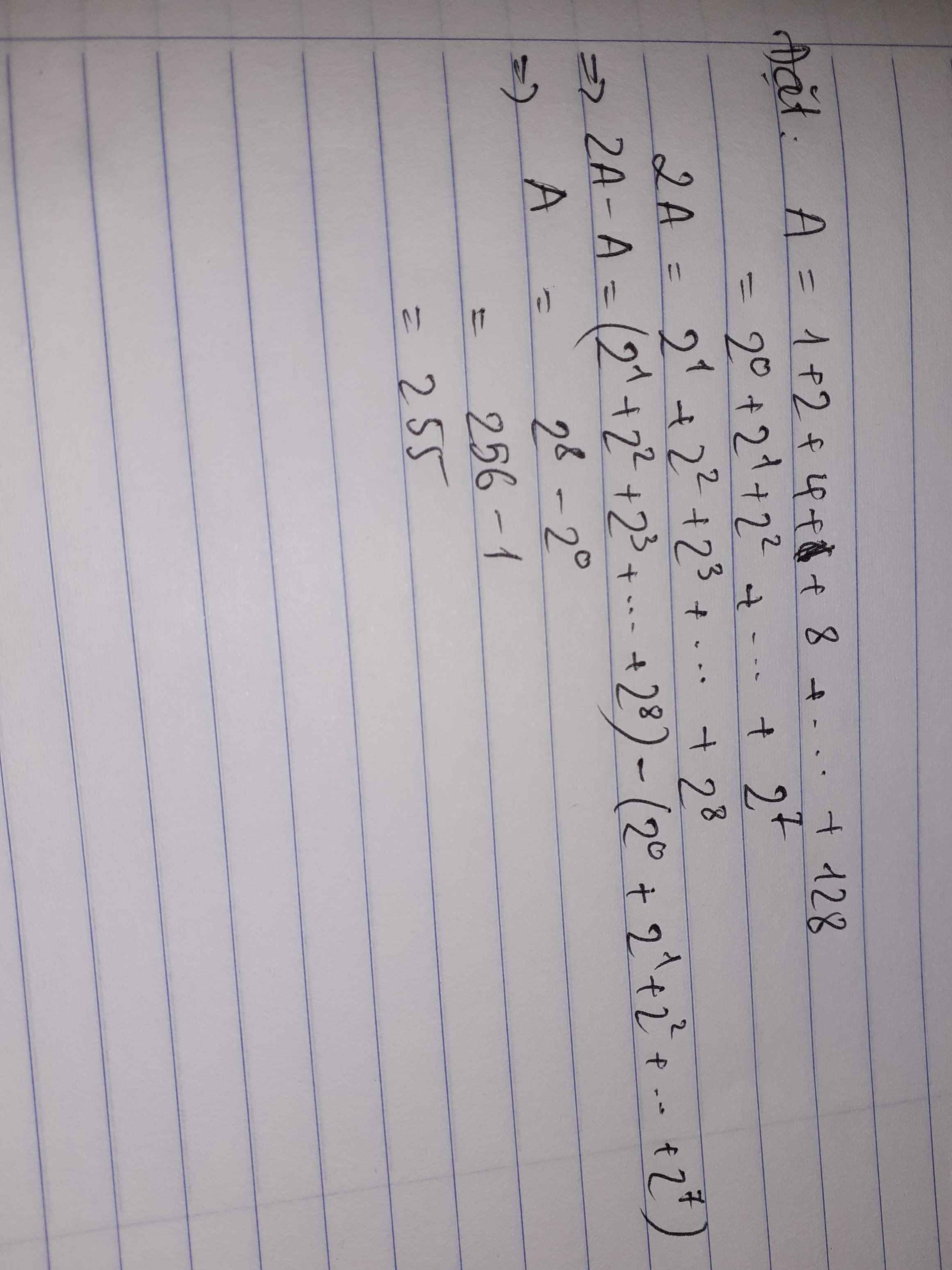
16
16