Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

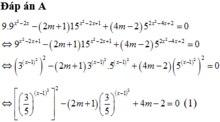

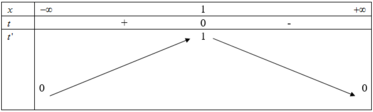
Dựa vào bảng biến thiên hàm f(x), ta thấy để phương trình (1) có 2 nghiệm thực x phân biệt thì phương trình (2) phải có duy nhất 1 nghiệm thuộc khoảng (0;1), nghiệm còn lại (nếu có) khác 1. Số nghiệm của (2) là số giao điểm của đồ thị hàm số y = 3 5 x - 1 2 và đường thẳng y = 2 m - 1 nên điều kiện của m thỏa mãn là 0 < 2 m - 1 < 1 ⇔ 1 2 < m < 1

Đáp án C
Phương pháp:
Đặt 2 x = t t > 0 , đưa về phương trình bậc 2 ẩn t, tìm điều kiện của phương trình bậc 2 ẩn t để phương trình ban đầu có 2 nghiệm phân biệt.
Cách giải: Đặt 2 x = t t > 0 khi đó phương trình trở thành t 2 − 2 m t + m + 2 = 0 *
Để phương trình ban đầu có 2 nghiệm phân biệt thì phương trình (*) có 2 nghiệm dương phân biệt.
Khi đó: Δ ' > 0 S > 0 P > 0 ⇔ m 2 − m − 2 > 0 2 m > 0 m + 2 > 0 ⇔ m > 2 m < − 1 m > 0 m > − 2 ⇒ m > 2
Chú ý và sai lầm: Rất nhiều học sinh sau khi đặt ẩn phụ thì quên mất điều kiện t > 0, dẫn đến việc chỉ đi tìm điều kiện đề phương trình (*) có 2 nghiệm phân biệt.


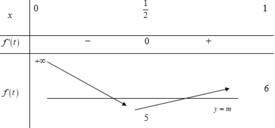
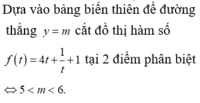




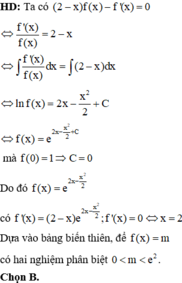


Chọn đáp án D
nên là hàm đồng biến trên từng khoảng xác định.