Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta có : y = 3 sin 2 x + cos 2 x sin 2 x + 4 cos 2 x + 1 = 3 sin 2 x + cos 2 x sin 2 x + 2 cos 2 x + 3
và sin 2 x + 2 cos 2 x + 3 > 0 ; ∀ x ∈ ℝ
xét phương trình
y = 3 sin 2 x + cos 2 x sin 2 x + 2 cos 2 x + 3
⇔ sin 2 x + 2 cos 2 x + 3 y = 3 sin 2 x + cos 2 x ⇔ y − 3 sin 2 x + 2 y − 1 cos 2 x = − 3 y
Phương trình trên có nghiệm nên
y − 3 2 + 2 y − 1 2 ≥ − 3 y 2 ⇔ 5 y 2 − 10 y + 10 ≥ 9 y 2
⇔ − 4 y 2 − 10 y + 10 ≥ 0 ⇔ − 5 − 65 4 ≤ y ≤ − 5 + 65 4
Suy ra giá trị lớn nhất của y là − 5 + 65 4
Phương trình 3 sin 2 x + cos 2 x sin 2 x + 2 cos 2 x + 3 ≤ m + 1 nghiệm đúngg với mọi số thực x khi
− 5 + 65 4 ≤ m + 1 ⇔ m ≥ − 9 + 65 4

Đáp án D
Ta có :
y = 3 sin 2 x + cos 2 x sin 2 x + 4 cos 2 x + 1 = 3 sin 2 x + cos 2 x sin 2 x + 2 cos 2 x + 3
Và sin 2 x + 2 cos 2 x + 3 > 0 ; ∀ x ∈ ℝ .
xét phương trình y = 3 sin 2 x + cos 2 x sin 2 x + 2 cos 2 x + 3
⇔ sin 2 x + 2 cos 2 x + 3 y = 3 sin 2 x + cos 2 x ⇔ y − 3 sin 2 x + 2 y − 1 cos 2 x = − 3 y
Phương trình trên có nghiệm nên
y − 3 2 + 2 y − 1 2 ≥ − 3 y 2 ⇔ 5 y 2 − 10 y + 10 ≥ 9 y 2
⇔ − 4 y 2 − 10 y + 10 ≥ 0 ⇔ − 5 − 65 4 ≤ y ≤ − 5 + 65 4
Suy ra giá trị lớn nhất của y là − 5 + 65 4
Phương trình 3 sin 2 x + cos 2 x sin 2 x + 2 cos 2 x + 3 ≤ m + 1 nghiệm đúngg với mọi số thực x khi − 5 + 65 4 ≤ m + 1 ⇔ m ≥ − 9 + 65 4

Đáp án C

Bảng biến thiên của hàm số f(x) là
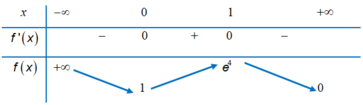
Hàm số f x là hàm số chẵn trên ℝ nên đồ thị của hàm số nhận trục tung làm trục đối xứng. Do đó phương trình f ( x ) + m = 0 có bốn nghiệm thực phân biệt khi và chỉ khi phương trình f ( x ) + m = 0 có hai nghiệm dương phân biệt hay phương trình f ( x ) = - m có hai nghiệm dương phân biệt
⇔ 1 < - m < e 4 ⇔ - e 4 < m < - 1
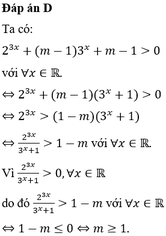




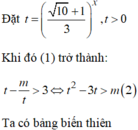
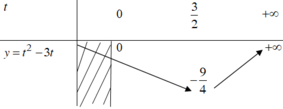

Đáp án D
B P T ⇔ 2 3 x + m − 1 3 x + m − 1 > 0 ⇔ 2 3 x − 3 x − 1 + m 3 x + 1 > 0 ⇔ m > 3 x − 8 x + 1 3 x + 1 ; ∀ x ∈ ℝ * .
Xét hàm số f x = 3 x − 8 x + 1 3 x + 1 ; ∀ x ∈ ℝ ,
ta có f ' x = 8 x ( ln 3 − ln 8 .3 x − ln 8 3 x + 1 2 < 0 ; ∀ x ∈ ℝ .
Suy ra f x là hàm số nghịch biến trên ℝ mà lim x → − ∞ f x = 1 , do đó min x ∈ ℝ f x = lim x → − ∞ f x = 1
Vậy * ⇔ m ≥ min x ∈ ℝ f x = 1 ⇒ m ≥ 1 là giá trị cần tìm.