Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
BPT <=> 23x + (m – 1)3x + m – 1 > 0
<=> 23x – 3x – 1 + m(3x + 1) > 0
⇔ m > 3 x - 8 x + 1 3 x + 1 ; ∀ x ∈ ℝ (*).
Xét hàm số f x = 3 x - 8 x + 1 3 x + 1 ; ∀ x ∈ ℝ , ta có
f ' x = 8 x ln 3 - ln 8 . 3 x - ln 8 3 x + 1 2 < 0 ; ∀ x ∈ ℝ .
Suy ra f(x) là hàm số nghịch biến trên ℝ .
Mà lim x → - ∞ f x = 1 , do đó
m i n x ∈ ℝ f x = lim x → - ∞ f x = 1 .
Vậy (*) ⇔ m ≥ m i n x ∈ ℝ f x = 1 ⇒ m ≥ 1 là giá trị cần tìm.

TH1: m=-1
BPT sẽ là:
-2(-1-1)x-3-3>0
=>4x-6>0
=>x>6/4
=>Loại
TH2: m<>-1
Δ=(2m-2)^2-4(m+1)(3m-3)
=4m^2-8m+4-4(3m^2-3)
=4m^2-8m+4-12m^2+12
=-8m^2-8m+16
Để BPT vô nghiệm thì -8m^2-8m+16<=0 và m+1<0
=>m^2+m-2>=0 và m<-1
=>(m+2)(m-1)>=0 và m<-1
=>(m>=1 hoặc m<=-2) và m<-1
=>m<=-2

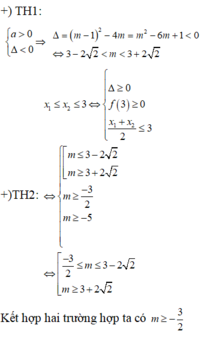
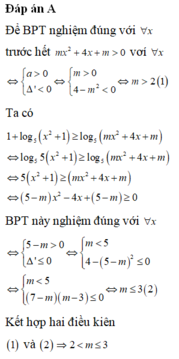



\(\Leftrightarrow\dfrac{3^x+3}{\sqrt{9^x+1}}=m\)
Đặt \(3^x=t>0\)
\(\Rightarrow\dfrac{t+3}{\sqrt{t^2+1}}=m\)
Xét hàm \(f\left(t\right)=\dfrac{t+3}{\sqrt{t^2+1}}\) khi \(t>0\) rồi lập BBT, từ đó xác định ra m có vẻ khá đơn giản