
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
`@-1 <= sin x <= 1`
`<=>0 <= 1+sin x <= 2=>1+sin x >= 0`
`@-1 <= cos x <= 1`
`<=>1 >= -cos x >= -1`
`<=>2 >= 1-cos x >= 0=>1-cos x >= 0`
Hàm số xác định `<=>[1+sin x]/[1-cos x] >= 0`
`<=>{(1+sin x >= 0(L Đ)),(1-cos x > 0):}<=>1-cos x ne 0<=>x ne k2\pi (k in ZZ)`
`=>TXĐ: D=R\\{k2\pi| k in ZZ}`.

\(y=\dfrac{cos3x}{1-sinx}+tanx=\dfrac{cos3x}{1-sinx}+\dfrac{sinx}{cosx}\)
Hàm số xác định khi \(\left\{{}\begin{matrix}1-sinx\ne0\\cosx\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}sinx\ne1\\cosx\ne0\end{matrix}\right.\Leftrightarrow x\ne\dfrac{\pi}{2}+k\pi\)

ĐK: \(\left\{{}\begin{matrix}sin\left(x-\dfrac{\pi}{4}\right)\ne0\\sin^4x-cos^4x\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-\dfrac{\pi}{4}\ne k\pi\\\left(cos^2x-sin^2x\right)\left(cos^2x+sin^2x\right)\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{4}+k\pi\\cos2x\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{4}+k\pi\\2x\ne\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{4}+k\pi\\x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\end{matrix}\right.\)
\(\Leftrightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)

1. Không dịch được đề
2.
\(-1\le cos2x\le1\Rightarrow1\le y\le3\)
3.
a. \(-2\le2sinx\le2\Rightarrow-1\le y\le3\)
\(y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
b.
\(0\le cos^2x\le1\Rightarrow-1\le y\le2\)
\(y_{min}=-1\) khi \(cos^2x=1\Rightarrow x=k\pi\)
\(y_{max}=2\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
4.
\(y=\left(tanx-1\right)^2+2\ge2\)
\(y_{min}=2\) khi \(tanx=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)

ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\cos\pi x\ne-1\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\pi x\ne\pi+k2\pi\)
\(\Leftrightarrow x\ne2k+1\)
Vậy \(\left\{{}\begin{matrix}x\ge0\\x\ne2k+1\left(k\in Z\right)\end{matrix}\right.\)

\(y=\dfrac{4}{3}\left(\sin^6x+\cos^6x\right)+\cos4x-1\)
\(\sin^6x+\cos^6x=\left(\sin^2x+\cos^2x\right)\left(\sin^4x-\sin^2x\cdot\cos^2x+\cos^4x\right)\\ =\left(\sin^2x+\cos^2x\right)^2-3\sin^2x\cdot\cos^2x=1-\dfrac{3}{4}\sin^22x\)
Do \(0\le\sin^22x\le1\Leftrightarrow\dfrac{3}{4}\cdot0\ge-\dfrac{3}{4}\sin^22x\ge-\dfrac{3}{4}\)
\(\Leftrightarrow1\ge1-\dfrac{3}{4}\sin^22x\ge1-\dfrac{3}{4}=\dfrac{1}{4}\\ \Leftrightarrow\dfrac{4}{3}\ge\dfrac{4}{3}\left(\sin^6x+\cos^6x\right)\ge\dfrac{1}{4}\cdot\dfrac{4}{3}=\dfrac{1}{3}\)
Ta có \(-1\le\cos4x\le1\)
\(\Leftrightarrow\dfrac{1}{3}-1-1\le\dfrac{4}{3}\left(\sin^6x+\cos^6x\right)+\cos4x-1\le\dfrac{4}{3}+1-1\\ \Leftrightarrow-\dfrac{5}{3}\le y\le\dfrac{4}{3}\)
Vậy \(y_{min}=-\dfrac{5}{3};y_{max}=\dfrac{4}{3}\)
\(y=\dfrac{4}{3}\left(sin^6x+cos^6x\right)+cos4x-1\)
\(y=\dfrac{4}{3}\left(\dfrac{5}{8}+\dfrac{3}{8}cos4x\right)+cos4x-1\)
\(y=\dfrac{3}{2}cos4x-\dfrac{1}{6}\)
\(-1\le cos4x\le1\Rightarrow-\dfrac{5}{3}\le y\le\dfrac{4}{3}\)
\(y_{min}=-\dfrac{5}{3}\) khi \(cos4x=-1\)
\(y_{max}=\dfrac{4}{3}\) khi \(cos4x=1\)

Ta có y= 2sin2x +1.
Do - 1 ≤ sin 2 x ≤ 1 ⇒ - 2 ≤ 2 sin 2 x ≤ 2
⇒ - 1 ≤ 2 sin 2 x + 1 ≤ 3 ⇒ - 1 ≤ y ≤ 3
Vậy giá trị lớn nhất của hàm số bằng , giá trị nhỏ nhất bằng .
Chọn C.

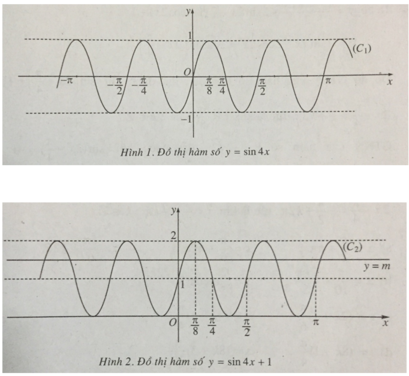
a) Ta có sin4(x + kπ/2) = sin(4x + k2π) = sin4x với k ∈ Z.
Từ đó suy ra hàm số y = sin4x là hàm số tuần hoàn với chu kì π/2.
Vì hàm số y = sin4x là hàm số lẻ nên đồ thị của nó có tâm đối xứng là gốc tọa độ O.
Các hàm số y = sin4x (C1) và y = sin4x + 1 (C2) có đồ thị như trên hình 1 và hình 2.
b) Vì sin4x + 1 = m ⇔ sin4x = m – 1
và -1 ≤ sin4x ≤ 1
nên -1 ≤ m – 1 ≤ 1
⇔ 0 ≤ m ≤ 2.
Từ đó, phương trình (1) có nghiệm khi 0 ≤ m ≤ 2 và vô nghiệm khi m > 2 hoặc m < 0.
c) Phương trình tiếp tuyến của (C2) có dạng
y - y o = y ’ ( x o ) ( x - x o ) .
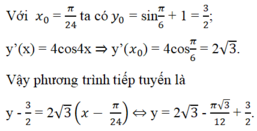
`y=sin^4 x+cos^4 x`
`y=(sin^2 x+cos^2 x)^2 -2sin^2 x.cos^2 x`
`y=1^2-1/2 . (2sin x.cos x)^2`
`y=1-1/2 sin 2x`
Ta có: `-1 <= sin 2x <= 1`
`<=>1/2 >= -1/2 sin 2x >= -1/2`
`<=>3/2 >= 1-1/2 sin 2x >= 1/2`
`=>` Tập giá trị của hàm số là: `T=[1/2;3/2]`.