Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\left(n+6\right)⋮\left(n+1\right)\Rightarrow\left(n+1\right)+5⋮\left(n+1\right)\)
\(\Rightarrow\left(n+1\right)\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\)
Do \(n\in N\)
\(\Rightarrow n\in\left\{0;4\right\}\)
b) \(\left(4n+9\right)⋮\left(2n+1\right)\Rightarrow2\left(2n+1\right)+7⋮\left(2n+1\right)\)
\(\Rightarrow\left(2n+1\right)\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\)
Do \(n\in N\)
\(\Rightarrow n\in\left\{0;3\right\}\)

Ta có: n+3 chia hết cho n-1
mà: n-1 chia hết cho n-1
suy ra:[(n+3)-(n-1)]chia hết cho n-1
(n+3-n+1)chia hết cho n-1
4 chia hết cho n-1
suy ra n-1 thuộc Ư(4)
Ư(4)={1;2;4}
suy ra n-1 thuộc {1;2;4}
Ta có bảng sau:
n-1 1 2 4
n 2 3 5
Vậy n=2 hoặc n=3 hoặc n=5

a,
Ta có: 4n-5 chia hết cho 2n-1
=>4n-2-3 chia hết cho 2n-1
=>2.(2n-1)-3 chia hết cho 2n-1
=>3 chia hết cho 2n-1
=>2n-1=Ư(3)=(-1,-3,1,3)
=>2n=(0,-2,2,4)
=>n=(0,-1,1,2)
Vậy n=0,-1,1,2

Để \(n^2+2n+7⋮n+2\)
\(\Rightarrow n\left(n+2\right)+7⋮n+2\)
Vì \(n\left(n+2\right)⋮n+2\Rightarrow7⋮n+2\Rightarrow n+2\inƯ\left(7\right)\Rightarrow n+2\in\left\{1;7\right\}\Rightarrow n\in\left\{-1;5\right\}\)
Để \(n^2+1⋮n-1\)
=> \(n^2-1+2⋮n-1\)
\(\Rightarrow\left(n^2-n+n-1\right)+2⋮n-1\)
\(\Rightarrow\left[n\left(n-1\right)+\left(n-1\right)\right]+2⋮n-1\)
=> (n - 1)(n + 1) + 2\(⋮n-1\)
Vì (n - 1)(n + 1) \(⋮n-1\)
=> 2\(2⋮n-1\Rightarrow n-1\inƯ\left(2\right)\Rightarrow n-1\in\left\{1;2\right\}\Rightarrow n\in\left\{2;3\right\}\)
Để \(n^2+2n+6⋮n+4\)
=> \(n^2+4n-2n-8+14⋮n+4\)
=> \(n\left(n+4\right)-2\left(n+4\right)+14⋮n+4\)
=> \(\left(n-2\right)\left(n+4\right)+14⋮n+4\)
Vì \(\left(n-2\right)\left(n+4\right)⋮n+4\)
=> \(14⋮n+4\Rightarrow n+4\inƯ\left(14\right)\Rightarrow n+4\in\left\{1;2;7;14\right\}\Rightarrow n\in\left\{-3;-2;3;10\right\}\)
Để n2 + n + 1 \(⋮n+1\)
=> \(n\left(n+1\right)+1⋮n+1\)
Vì \(n\left(n+1\right)⋮n+1\)
=> \(1⋮n+1\Rightarrow n+1\inƯ\left(1\right)\Rightarrow n+1=1\Rightarrow n=0\)

bài 4
Các số chia hết cho 2 nhưng không chia hết cho 5 có tận cùng 2, 4, 6, 8 ; mỗi chục có bốn số đó.
Từ 0 đến 999 có 100 chục nên có :
4.100 = 400 (số).
Vậy trong các số tự nhiên nhỏ hơn 1000, có 400 số chia hết cho 2 nhưng ko chia hết cho 5
bài 5
Gọi thương của số tự nhiên x tuần tự là a và b
Theo đề, ta có:
x = 4a + 1
x = 25b + 3
<=> 4a + 1 = 25b + 3
4a = 25b + 2
a = (25b + 2)/4
b = 2 ; a = 13 <=> x = 53
b = 6 ; a = 38 <=> x = 153
b = 10 ; a = 63 <=> x = 253
b = 14 ; a = 88 <=> x = 353
b = 18 ; a = 113 <=> x = 453
Đáp số: Tất cả các số tự nhiên, tận cùng là 53 đều thoả mãn điều kiện.

. .......................................................................................................................................jjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjj

\(a,\Rightarrow n+3\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Rightarrow n\in\left\{-8;-4;-2;2\right\}\\ b,\Rightarrow n+3+5⋮n+3\\ \Rightarrow5⋮n+3\\ \Rightarrow n+3\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Rightarrow n\in\left\{-8;-4;-2;2\right\}\\ c,\Rightarrow2\left(2n-1\right)-3⋮2n-1\\ \Rightarrow3⋮2n-1\\ \Rightarrow2n-1\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\\ \Rightarrow n\in\left\{-1;0;1;2\right\}\\ d,\Rightarrow8-n+4⋮8-n\\ \Rightarrow4⋮8-n\\ \Rightarrow8-n\inƯ\left(4\right)=\left\{-4;-2;-1;1;2;4\right\}\\ \Rightarrow n\in\left\{12;10;9;7;6;4\right\}\)
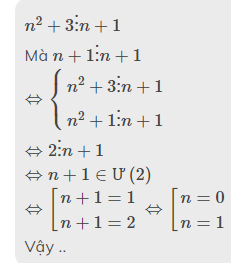
a) n+2 chia hết cho n-1
=>n-1+3 chia hết cho n-1
Vì n-1 chia hết cho n-1
=>3 chia hết cho n-1
=>n-1\(\in\)Ư(3)
=>n-1\(\in\){-3;-1;1;3}
=>n\(\in\){-2;0;2;4}
Vì n là số tự nhiên nên n\(\in\){0;2;4}
b)2n+1 chia hết cho 6-n
Bởi n-6 là số đối của 6-n
=>2n+1 cũng chia hết cho n-6
=>2n-12+13 chia hết cho n-6
=>2(n-6) +13 chia hết cho n-6
Mà 2(n-6) chia hết cho n-6
=>13 chia hết cho n-6
=>n-6\(\in\)Ư(13)
=>n-6\(\in\){-13;-1;1;13}
=>n\(\in\){-7;5;7;19}
Vì n là số tự nhiên nên n\(\in\){5;7;19} (câu này ko chắc lắm đâu)
b)=5