Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi phân số cần tìm là a/b
Ta có a/b:14/9=n;a/b:45/27=m(m,nEN)
=> a/b*9/14=n;a/b*3/5=m(vì27/45=3/5)
=> 9a/14b=n;3a/5b=m
Mà ƯCLN(9;14)=1 Nên a chia hết cho 14;9 chia hết cho b(1)
ƯCLN(3,5)=1 Nên a chia hết cho 5;3 chia hết cho b(2)
Từ (1) và (2) =>aEBC(5;14);bEƯC(9;3)
Mà a/b nhỏ nhất Nên a nhỏ nhất và b lớn nhất
=>a EBCNN(5;14);bEƯCLN(9;3)
=>a=70;b=3
Vậy phân số cần tìm là 70/3

Do 2n+1 là số chính phương lẻ nên 2n+1 chia cho 8 dư 1.
=> n chia hết cho 4. => 3n+1 cũng là một số chính phương lẻ(Do 3n+1 là số chính phương).
=> 3n+1 chia cho 8 dư 1. => 3n chia hết cho 8.
=> n chia hết cho 8( Do (3,8)=1). (1)
-Ta có: 2n+1 và 3n+1 là hai đô chính phương. +Nếu n chia cho 5 dư 4=> 3n+1 chia cho 5 dư 3. => Loại do
số chính phương chia cho 5 chỉ dư 0;1;4. +Nếu n chia cho 5 dư 3=> 2n+1 chia cho 5 dư 2. => Loại.
+Nếu n chia cho 5 dư 2=> 3n+1 chia cho 5 dư 2. => Loại.
+Nếu n chia cho 5 dư 1=> 2n+1 chia cho 5 dư 3. => Loại.
-Từ 4 điều trên và n có tồn tại => n chia hết cho 5. (2)
-Từ (1);(2) => n chia hết cho 8.5= 40.( Do (8,5)=1).
=>n=40 hoặc n=80
Với n=40 =>2n+1 là số chính phương
Với n=80 =>2n+1 không phải là số chính phương
Vậy n=40

Đáp án C.
Mỗi mặt sẽ có 4 phần thuộc hình chỉ được tô một lần tức là mỗi mặt sẽ sinh ra 4 hình lập phương thỏa mãn yêu cầu bài toán, ta có 6 mặt, từ đó ta có 24 hình thỏa mãn yêu cầu.


Đáp án C.
Mỗi mặt sẽ có 4 phần thuộc hình chỉ được tô một lần tức là mỗi mặt sẽ sinh ra 4 hình lập phương thỏa mãn yêu cầu bài toán, ta có 6 mặt, từ đó ta có 24 hình thỏa mãn yêu cầu
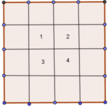

Đáp án D
Phương pháp: Gắn hệ trục tọa độ Oxyz để giải bài toán.
Cách giải: Giả sử mặt phẳng chứa AC’ cắt hình lập phương theo thiết diện là tứ giác AEC’F ![]()
Ta có: 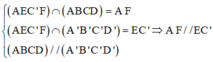
Tương tự ta chứng minh được AE//FC’
=>AEC’ F là hình bình hành ![]()
Gắn hệ trục tọa độ như hình vẽ sao cho A’(0;0;0); B’(2;0;0); C’(2;2;0); D’(0;2;0); A(0;0;2); B(2;0;2); C(2;2;2); D(0;2;2)
Gọi E(x;0;0) (0≤x≤2) ta có:
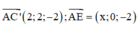
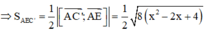
Ta có ![]()
Dấu bằng xảy ra ó x = 1, khi đó ![]()

Đáp án D
Giả sử (P) cắt cạnh AA’ tại M sao cho A'M = x
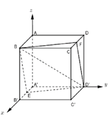
Chọn hệ trục tọa độ như hình vẽ
B(0;0;1), D'(1;1;0), M(1;0;x)
B D ' → 1 ; 1 ; - 1 , B M → 0 ; - 1 ; x + 1 ⇒ B D ' → , B M → = x ; - x - 1 ; - 1
Thiết diện BMD’N thu được là hình bình hành nên
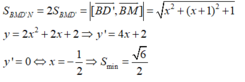

Đáp án D
Giả sử (P) cắt cạnh AA’ tại M sao cho A'M = x
Chọn hệ trục tọa độ như hình vẽ
B ( 0 ; 0 ; 1 ) , D ' ( 1 ; 1 ; 0 ) , M ( 1 ; 0 ; x ) ⇒ B D ' → ( 1 ; 1 ; − 1 ) , B M → ( 0 ; − 1 ; x + 1 ) ⇒ [ B D ' → , B M → ] = ( x ; − x − 1 ; − 1 )
Thiết diện BMD’N thu được là hình bình hành nên
S B M D ' N = 2 S B M D ' = [ B D ' → , B M → ] = x 2 + ( x + 1 ) 2 + 1 y = 2 x 2 + 2 x + 2 ⇒ y ' = 4 x + 2 y ' = 0 ⇔ x = − 1 2 ⇒ S min = 6 2

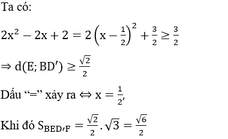
2n là số chính phương =>
n=2k2\(\)\(\)=>3n=6k2
3n là số lập phương Suy ra 6=k.a3
n nhỏ nhất suy ra a=1 => k=6 => n=72[/QUOTE]