Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có
n 360 < 3 480 ⇔ ln n 360 < ln 3 480 ⇔ 360. ln n < 480. ln 3 ⇔ ln n < 4 3 . ln 3 ⇔ n < e 4 3 ln 3 ≈ 4 , 326.
Vậy giá trị nguyên n lớn nhất thỏa mãn là n = 4.

Lời giải:
Ta có $3^m+5^n\equiv 3^m+1\equiv 0\pmod 4$ nên $3^m\equiv (-1)^m\equiv -1\pmod 4$ nên $m$ lẻ
Đặt $m=2k+1$ ( $k\in\mathbb{N}$) thì $3^m=3^{2k+1}\equiv 3\pmod 8$
$\Rightarrow 5^n\equiv 5\pmod 8$. Xét tính chẵn, lẻ ( đặt $n=2t,2t+1$) suy ra $n$ lẻ
Do đó $\Rightarrow 3^n+5^m\equiv (-5)^n+(-3)^m=-(5^n+3^m)\equiv 0\pmod 8$
Ta có đpcm


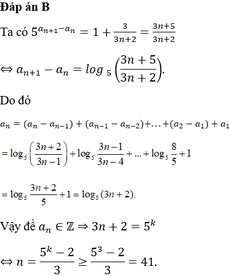

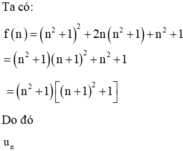
Đáp án B
Ta có: n 360 < n 480 ⇔ ln n 360 < ln 3 480
⇔ 360. ln n > 480. ln 3 ⇔ ln n < 4 3 . ln 3 ⇔ n < e 4 3 ln 3 ≈ 4 , 326.
Vậy giá trị nguyên n lớn nhất thỏa mãn là n=4