K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PN
tìm số nguyên dương n, biết:
a) 25<5n<625
b)3.27>3nlớn hơn, bằng 9
c)16 bé hơn, bằng 8n bé hơn, bằng 64
1
21 tháng 2 2020
a) \(25< 5^n< 625\)
\(25=5^2;625=5^4\)
=> \(5^2< 5^n< 5^4\)
=> 2 < n < 4
=> n = 3
b) \(9\le3^n< 3.27\)
\(9=3^2;3.27=3.3^3=3^4\)
=> \(3^2\le3^n< 3^4\)
=> n = 2; hoặc n = 3
c) \(16\le8^n\le64\)
\(16=8.2;64=8^2\)
=> \(8.2\le8^n\le8^2\)
=> n = 2
NT
1
15 tháng 8 2021
Ta có: \(8^{n+2}+8^n-5^{n+2}-5^n\)
\(=8^n\left(64+1\right)-5^n\left(5^2+1\right)\)
\(=8^n\cdot65-5^{n-1}\cdot130⋮65\)
CC
2
M
19 tháng 9 2017
(1/32)n.16n=1024-1
=> (1/32.16)n=1/1024
=> (1/2)n=1/1024
=> (1/2)n=(1/2)10
=> n=10
DD
Đoàn Đức Hà
Giáo viên
17 tháng 1 2021
a) \(n^2+8n+29=n^2+4n+4n+16+15=\left(n+4\right)^2+15=m^2\)
\(\Leftrightarrow m^2-\left(n+4\right)^2=15\Leftrightarrow\left(m-n-4\right)\left(m+n+4\right)=13=1.13\)
Do \(m-n-4< m+n+4\)nên ta có trường hợp:
\(\hept{\begin{cases}m-n-4=1\\m+n+4=13\end{cases}}\Leftrightarrow\hept{\begin{cases}m=7\\n=2\end{cases}}\)(thỏa)
b) \(9n^2+6n+22=3\left(3n^2+n\right)+3n+1+21=\left(3n+1\right)^2+21=m^2\)
\(\Leftrightarrow m^2-\left(3n+1\right)^2=21\Leftrightarrow\left(m-3n-1\right)\left(m+3n+1\right)=21=1.21=3.7\)
Ta có các trường hợp:
- \(\hept{\begin{cases}m-3n-1=1\\m+3n+1=21\end{cases}}\Leftrightarrow\hept{\begin{cases}m=11\\n=3\end{cases}}\)(thỏa)
- \(\hept{\begin{cases}m-3n-1=3\\m+3n+1=7\end{cases}}\Leftrightarrow\hept{\begin{cases}m=5\\n=\frac{1}{3}\end{cases}}\)(loại)
LL
0
M
4
VT
1
22 tháng 11 2019
Câu hỏi của Tiểu thư họ Vũ - Toán lớp 9 - Học toán với OnlineMath
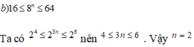
Từ đề bài suy ra 24 ≤ 23n ≤ 26, tìm được n = 2