F
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MH
28 tháng 12 2021
\(B=3+3^2+3^3+3^4+...+3^{2009}+3^{2010}\)
\(=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{2009}+3^{2010}\right)\)
\(=3\left(1+3\right)+3^3\left(1+3\right)+...+3^{2009}\left(1+3\right)\)
\(=4.\left(3+3^3+...+3^{2009}\right)\)
⇒ \(B\) ⋮ 4
29 tháng 12 2021
b: \(C=5\left(1+5+5^2\right)+...+5^{2008}\left(1+5+5^2\right)=31\cdot\left(5+...+5^{2008}\right)⋮31\)
13 tháng 2 2022
a. S = 5 + 52 + 53 + 54 + 55 + 56 +...+ 52012.
S = (5 + 52 + 53 + 54) + 55(5 + 52 + 53 + 54)+....+ 52009(5 + 52 + 53 + 54)
Vì (5 + 52 + 53 + 54) = 780 chia hết cho 65
Vậy S chia hết cho 65
b. Gọi số cần tìm là a ta có: (a - 6) chia hết cho 11; (a - 1) chia hết cho 4; (a - 11) chia hết cho 19.
(a - 6 + 33) chia hết cho 11; (a - 1 + 28) chia hết cho 4; (a - 11 + 38) chia hết cho 19.
(a + 27) chia hết cho 11; (a + 27) chia hết cho 4; (a + 27) chia hết cho 19.
Do a là số tự nhiên nhỏ nhất nên a + 27 nhỏ nhất
Suy ra: a + 27 = BCNN (4;11; 19).
Từ đó tìm được: a = 809
A = 10n + 18n - 1 = 10n - 1 - 9n + 27n
PT
24 tháng 1 2021
a. S = 5 + 52 + 53 + 54 + 55 + 56 +...+ 52012.
S = (5 + 52 + 53 + 54) + 55(5 + 52 + 53 + 54)+....+ 52009(5 + 52 + 53 + 54)
Vì (5 + 52 + 53 + 54) = 780 chia hết cho 65
Vậy S chia hết cho 65
b. Gọi số cần tìm là a ta có: (a - 6) chia hết cho 11; (a - 1) chia hết cho 4; (a - 11) chia hết cho 19.
(a - 6 + 33) chia hết cho 11; (a - 1 + 28) chia hết cho 4; (a - 11 + 38) chia hết cho 19.
(a + 27) chia hết cho 11; (a + 27) chia hết cho 4; (a + 27) chia hết cho 19.
Do a là số tự nhiên nhỏ nhất nên a + 27 nhỏ nhất
Suy ra: a + 27 = BCNN (4;11; 19).
Từ đó tìm được: a = 809
A = 10n + 18n - 1 = 10n - 1 - 9n + 27n
Ta biết số n và số có tổng các chữ số bằng n có cùng số dư khi chia cho 9 do đó 
nên 
* Vậy A chia hết cho 27
AH
Akai Haruma
Giáo viên
13 tháng 12 2022
Lời giải:
a. $(x-3)(y+1)=5=1.5=5.1=(-1)(-5)=(-5)(-1)$
Vì $x-3, y+1$ cũng là số nguyên nên ta có bảng sau:
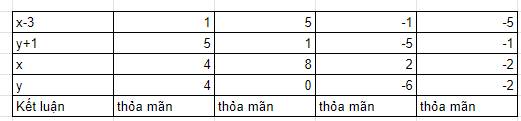
b.
$A=21+5+(5^2+5^3)+(5^4+5^5)+....+(5^{98}+5^{99})$
$=26+5^2(1+5)+5^4(1+5)+....+5^{98}(1+5)$
$=2+24+(1+5)(5^2+5^4+...+5^{98}$
$=2+24+6(5^2+5^4+....+5^{98})=2+6(4+5^2+5^4+...+5^{98})$
$\Rightarrow A$ chia $6$ dư $2$.
PN
0
PN
1
21 tháng 11 2021
\(=5+\left(5^2+5^3\right)+\left(5^4+5^5\right)+...+\left(5^{2020}+5^{2021}\right)\\ =5+5\left(5+5^2\right)+5^3\left(5+5^2\right)+...+5^{2019}\left(5+5^2\right)\\ =5+\left(5+5^2\right)\left(5+5^3+...+5^{2019}\right)\\ =5+31\left(5+5^3+...+5^{2019}\right)\)
Vậy BT chia 31 dư 5
NV
2
H9
HT.Phong (9A5)
CTVHS
7 tháng 10 2023
\(A=5+5^2+5^3+...+5^{20}\)
\(A=\left(5+5^2\right)+\left(5^3+5^4+5^5\right)+...+\left(5^{18}+5^{19}+5^{20}\right)\)
\(A=30+5^3\cdot31+...+5^{18}\cdot31\)
\(A=30+31\cdot\left(5^3+5^6+...+5^{18}\right)\)
Mà: \(31\cdot\left(5^3+5^6+...+5^{18}\right)\) ⋮ 31
\(\Rightarrow A=30+31\cdot\left(5^3+5^6+...+5^{18}\right)\) chia cho 31 dư 30
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
7 tháng 10 2023
A = 5 + 52 + 53 +...+ 520
A = 520 + 519 + 518 +...+ 53 + 52 + 5
A = (520 + 519 + 518) + (517 + 516 + 515) +...+ (55 + 54 + 53) + (52+ 5)
A = 518.( 52 + 5 + 1) + 515.(52 + 5 + 1) +...+ 53.(52+ 5 + 1) + (25 + 5)
A = 518. 31 + 515.31 +...+ 53.31 + 30
A = 31.(518 + 515 +...+ 53) + 30
31 ⋮ 31 ⇒ 31.(518 + 515 +...+53) ⋮ 31 mà 30 : 31 = 0 dư 31
Vậy A : 31 dư 30
NM
4
BD
29 tháng 6 2023
0\(a.S=1-5+5^2-5^3+...+5^{98}-5^{99}\\ 5S=5-5^2+5^3-5^4+.....+5^{99}-5^{100}\\ 5S+S=\left(5-5^2+5^3-5^4+.....+5^{99}-5^{100}\right)+\left(1-5^{ }+5^2-5^3+.....+5^{98}-5^{99}\right)\\ 6S=1-5^{100}\\ S=\dfrac{1-5^{100}}{6}\\ \)
\(b,S6=1-5^{100}\\ 1-S6=5^{100}\)
=> 5100 chia 6 du 1
PD
1
29 tháng 11 2023
Bài 1:
a: \(S=1-5+5^2-5^3+...+5^{98}-5^{99}\)
=>\(5S=5-5^2+5^3-5^4+...+5^{99}-5^{100}\)
=>\(6S=5-5^2+5^3-5^4+...+5^{99}-5^{100}+1-5+5^2-5^3+...+5^{98}-5^{99}\)
=>\(6S=-5^{100}+1\)
=>\(S=\dfrac{-5^{100}+1}{6}\)
b: S=1-5+52-53+...+598-599 là số nguyên
=>\(\dfrac{-5^{100}+1}{6}\in Z\)
=>\(-5^{100}+1⋮6\)
=>\(5^{100}-1⋮6\)
=>\(5^{100}\) chia 6 dư 1
Ta có :
\(S=1+5+5^2+5^3+5^4+5^5+5^6+5^7+5^8+5^9\)
\(\Rightarrow S=1+\left(5+5^2+5^3\right)+\left(5^4+5^5+5^6\right)+\left(5^7+5^8+5^9\right)\)
\(\Rightarrow S=1+5\left(1+5+5^2\right)+5^4\left(1+5+5^2\right)+5^7\left(1+5+5^2\right)\)
\(\Rightarrow S=1+5.31+5^4.31+5^7.31\)
\(\Rightarrow S=1+31\left(5+5^4+5^7\right)\)
Vậy \(S:31\)dư \(1\)
\(S=1+5+5^2+5^3+...+5^9\)
Đặt \(A=5+5^2+5^3+...+5^9\)
\(=\left(5+5^2+5^3\right)+...+\left(5^7+5^8+5^9\right)\)
\(=\left(5.1+5.5+5.5^2\right)+...+\left(5^7.1+5^7.5+5^7.5^2\right)\)
\(=5.\left(1+5+5^2\right)+...+5^7.\left(1+5+5^2\right)\)
\(=5.31+...+5^7.31\)
\(=\left(5+5^7\right).31\)
Thay A vào S, ta có:
\(S=1+\left(5+5^7\right).31\)
Vì \(\left(5+5^7\right).31⋮31\)mà \(S=1+\left(5+5^7\right).31\)
Suy ra S chia cho 31 dư 1.
hok tốt nha !