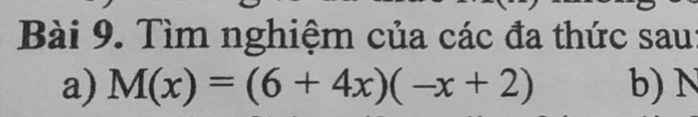Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(3x^3+4x^2+2x+1=0\)
\(\Leftrightarrow\left(3x^3+x^2+x\right)+\left(3x^2+x+1\right)=0\)
\(\Leftrightarrow x\left(3x^2+x+1\right)+1\left(3x^2+x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x^2+x+1\right)=0\)
Ta có:\(3x^2+x+1=3\left(x^2+x.\frac{1}{3}+\frac{1}{3}\right)\)
\(=3\left(x^2+2.x.\frac{1}{6}+\frac{1}{36}-\frac{1}{36}+\frac{1}{3}\right)\)
\(=3\left[\left(x+\frac{1}{6}\right)^2+\frac{11}{36}\right]\ge3.\frac{11}{36}=\frac{11}{12}>0\forall x\)
Do đó x + 1 = 0 tức là x = -1
\(3x^3+3x^2+x^2+x+x+1=0\)
\(3x^2.\left(x+1\right)+x.\left(x+1\right)+\left(x+1\right)=0\)
\(\left(x+1\right).\left(3x^2+x+1\right)=0\)
+)\(3x^2+x+1=0\Leftrightarrow3.\left(x^2+x+\frac{1}{3}\right)=0\Leftrightarrow3.\left(x+\frac{1}{6}\right)^2+\frac{11}{12}=0\left(loai\right)\)
+) x+1=0 <=> x=-1

Lời giải:
$M(x)=(6+4x)(-x+2)=0$
\(\Leftrightarrow \left[\begin{matrix} 6+4x=0\\ -x+2=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=-\frac{3}{2}\\ x=2\end{matrix}\right.\)
Vậy nghiệm của đa thức $M(x)$ là $x=\frac{-3}{2}$ và $x=2$

a)g(x)=0=>11x3+5x2+4x+10=0
=>(10x3+10)+(x3+x2)+(4x2+4x)=0
=>10(x3+1)+x2(x+1)+4x(x+1)=0
=>10(x+1)(x2−x+1)+x2(x+1)+4x(x+1)=0
=>(x+1)[(10(x2−x+1)+x2+4x]=0
=>(x+1)(11x2−6x+10)=0
=>(x+1)[(9x2−2.3x+1)+2x2+9]=0
=>(x+1)[(3x−1)2+2x2+9]=0
=>x+1=0
=>x=-1
Vậy x=-1

a) Thay đa thức này bằng 0, ta được:
f(x) = x^3 - x^2 + x - 1 = 0
=> f(x) = x . x2 - x . x + x - 1 = 0
=> f(x) = x. (x2 - x + x) = 0 + 1 = 1
=> f(x) = x . x2 = 1
=> x = 1 và x2 = 1
=> x = 1
Vậy nghiệm của đa thức là x = 1

4x2 + x - 3 = 0
<=> 4x2 + 4x - 3x - 3 = 0
<=> 4(x + 1) - 3(x + 1) = 0
<=> (x + 1)(4x - 3) = 0
<=> \(\orbr{\begin{cases}x+1=0\\4x-3=0\end{cases}}\)<=> \(\orbr{\begin{cases}x=-1\\x=\frac{3}{4}\end{cases}}\)
Vậy: x = -1; x = 3/4 là nghiệm của đa thức 4x2 + x - 3

\(x^2-5x+6=0\)
\(x^2-2x-3x+6=0\)
\(x\left(x-2\right)-3\left(x-2\right)=0\)
\(\left(x-3\right)\left(x-2\right)=0\)
- \(x-3=0\)
\(x=3\)
- \(x-2=0\)
\(x=2\)
Vậy x = 3 và x = 2 là nghiệm của đa thức trên. (cái đa thức kia bạn ghi rõ lại hơn đi)

\(2x^2-4x+5=2\left(x^2-2x+\frac{5}{2}\right)=2\left[\left(x^2-2x+1\right)+\frac{3}{2}\right]=2\left[\left(x-1\right)^2+\frac{3}{2}\right]=2\left(x-1\right)^2+3\ge3\)
\(\Rightarrow x\in\phi\)

\(P\left(x\right)=2x^3+4x^2-5x-1=0\)
<=> \(2x^3-2x^2+6x^2-6x+x-1=0\)
<=> \(2x^2\left(x-1\right)+6x\left(x-1\right)+x-1=0\)
<=> \(\left(x-1\right)\left(2x^2+6x+1\right)=0\)
<=> \(x-1=0\) (do 2x2 + 6x + 1 khác 0)
<=> \(x=1\)
Vậy....
\(P\left(x\right)=2x^3+4x^2-5x-1\)
\(P\left(x\right)=2x^3-2x^2+6x^2-6x+x-1\)
\(P\left(x\right)=2x^2\left(x-1\right)-6x\left(x-1\right)+\left(x-1\right)\)
\(P\left(x\right)=\left(x-1\right)\left(2x^2-6x+1\right)\)
Để P(x) có nghiệm \(\Rightarrow x-1=0\Leftrightarrow x=1\)
Vậy x = 1 là 1 nghiệm của P(x)