Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


n + 3 ⋮ 7
=> n + 3 + 7 ⋮ 7
=> n + 10 ⋮ 7
=> n + 10 ∈ B(7)
=> n + 10 = 7k (k ∈ N)
=> n = 7k - 10 (k ∈ N)
Vậy n có dạng là 7k - 10 (k ∈ N)
n+3chia hết7
=>n+3 thuộc Ư(7)={1;7}
ta có
n+3=1 n+3=7
n= -2(loại) n=4
vậy n=4

Đặt \(\frac{n^2}{180-n}\)= P ( P nguyên tố )
=> n2 = P . (180 - n ) => n2 chia hết cho P => n chia hết cho P
=> n = K . P( K thuộc N sao ) thay vào trên ta có :
(K . P)2 = P . ( 180 - K . P )
K2 .P2 = 180 .P - K.P2
K2.P2 +KP2 = 180 .P
K(K + 1) = 180 = 22 . 32 . 5
Do P là số nguyên tố nên P thuộc { 2,3,5}
+> Nếu P = 2 ta có : K .( K+1) =2. 32 . 5 = 90=> K = 90
Khi đó n = 9 .2 =18
+> Nếu P = 3 ta có : K ( K + 1 ) = 22 . 3. 5 = 60 => K thuộc tập hợp rỗng
+> Nếu P = 5 ta có : K ( K +1 ) =22.32 = 36 => K thuộc tập hợp rỗng
Vậy n = 18

Bài 2:
a: \(\Leftrightarrow3n-3+10⋮n-1\)
\(\Leftrightarrow n-1\in\left\{-1;1;2;5;10\right\}\)
hay \(n\in\left\{0;2;3;6;11\right\}\)
b: \(\Leftrightarrow n^2-1+9⋮n+1\)
\(\Leftrightarrow n+1\in\left\{1;3;9\right\}\)
hay \(n\in\left\{0;2;8\right\}\)

Vì n và n+1 là 2 số liên tiếp
=>n và n+1 là 2 số nguyên tố cùng nhau
=>ƯCLN(n,n+1)=1
=>n/n+1 là phân số tối giản
Gọi d = ƯCLN(n;n+1) \(\Rightarrow\hept{\begin{cases}n⋮d\\n+1⋮d\end{cases}}\Rightarrow n+1-n⋮d\Rightarrow1⋮d\Rightarrow d=\pm1\)
Vậy \(\frac{n}{n+1}\)là phân số tối giản \(\forall n\in N\)

a )Để A là phân số <=> \(\frac{n-2}{n+3}\) là phân số => \(n+3\ne0\Rightarrow n\ne-3\)
b ) \(A=\frac{n-2}{n+3}=\frac{n+3-5}{n+3}=\frac{n+3}{n+3}-\frac{5}{n+3}=1-\frac{5}{n+3}\)
Để \(1-\frac{5}{n+3}\) là số nguyên <=> \(\frac{5}{n+3}\) là số nguyên
=> n + 3 thuộc Ư(5) = { - 5; - 1; 1; 5 }
=> n + 3 = { - 5; - 1; 1; 5 }
=> n = { - 8; - 4; - 2 ; 2 }
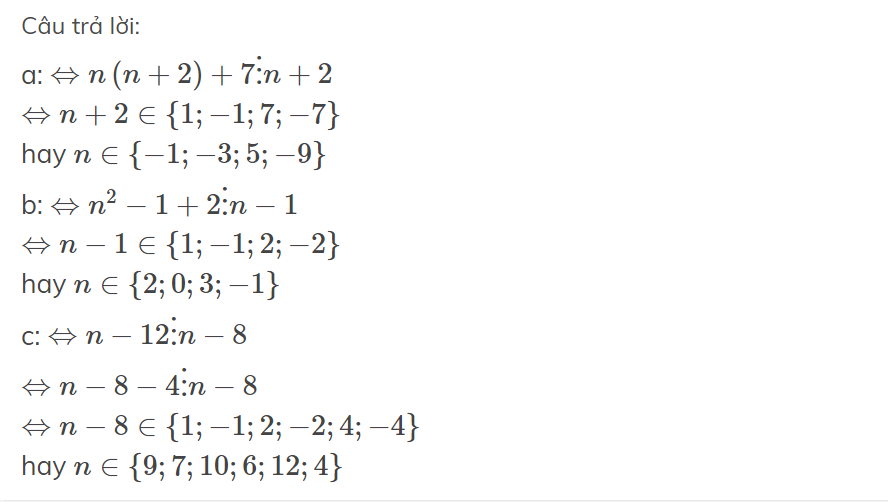
n - 6 là ước của n + 1
<=> n - 6 chia hết cho n + 1
<=> n + 1 - 7 chia hết cho n + 1
<=> - 7 chia hết cho n + 1
<=> n + 1 thuộc Ư(-7) = {-7 ; -1 ; 1 ; 7}
<=> n thuộc {-8 ; -2 ; 0 ; 6}
câu này à