Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Dự đoán dấu "=" xảy ra khi x = y. Gộp một cách hợp lí các số hạng để áp dụng bất đẳng thức.
\(A=\frac{1}{x^2+y^2}+\frac{1}{2xy}+\frac{1}{2xy}\ge\frac{4}{x^2+y^2+2xy}+\frac{1}{2.\frac{\left(x+y\right)^2}{4}}=\frac{4}{\left(x+y\right)^2}+\frac{2}{\left(x+y\right)^2}=6\)
Dấu "=" xảy ra khi x = y = 1/2.
GTNN của A là 6.
\(B=\frac{1}{x^2+y^2}+\frac{1}{2xy}+\frac{1}{4xy}+4xy+\frac{8057}{4xy}\)
\(\ge\frac{4}{x^2+y^2+2xy}+2\sqrt{\frac{1}{4xy}.4xy}+\frac{8057}{\left(x+y\right)^2}=\frac{4}{\left(x+y\right)^2}+2+\frac{8057}{\left(x+y\right)^2}=8063\)
Dấu "=" xảy ra khi x = y = 1/2.
Vậy GTNN của B là 8063.

1: Xét tứ giác BHCK có
CH//BK
BH//CK
Do đó: BHCK là hình bình hành
Suy ra: Hai đường chéo BC và HK cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HK
2: Gọi giao điểm của IH và BC là O
Suy ra: IH\(\perp\)BC tại O và O là trung điểm của IH
Xét ΔHIK có
O là trung điểm của HI
M là trung điểm của HK
Do đó: OM là đường trung bình của ΔHIK
Suy ra: OM//IK
hay BC//IK
mà BC\(\perp\)IH
nên IH\(\perp\)IK
Xét ΔHOC vuông tại O và ΔIOC vuông tại O có
OC chung
HO=IO
Do đó: ΔHOC=ΔIOC
Suy ra: CH=CI
mà CH=BK
nên CI=BK
Xét tứ giác BCKI có IK//BC
nên BCKI là hình thang
mà CI=BK
nên BCKI là hình thang cân

Xét tam giác ODC có:
AB/CD=1/2 (gt)
OA/OC=1/2 (OA/AC=1/3)
=>AB//CD(d/l Ta-lét)
=> ABCD là hình thang
=> bạn hãy cố gắng làm tiếp nếu có thể
hãy tìm các cặp diện tích tam giác bằng nhau, chứ mik ko chắc nữa

a) \(\left(7-14x\right)\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}7-14x=0\\x-2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}14x=7-0\\x=2\end{cases}\Leftrightarrow}}\orbr{\begin{cases}14x=7\\x=2\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{1}{2}\\x=2\end{cases}}}\)
Vậy \(x\in\left\{\frac{1}{2};2\right\}\)
b) \(\left(2x+1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x+1=0\\x-3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}2x=-1\\x=3\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=\frac{-1}{2}\\x=3\end{cases}}}\)
Vậy \(x\in\left\{-\frac{1}{2};3\right\}\)

\(\left(x-3\right)\left(x^2+3x+9\right)+x\left(x+2\right)\left(2-x\right)=1\)
\(x^3-3^3+x\left(2^2-x^2\right)=1\)
\(x^3-27+4x-x^3=1\)
\(4x-27=1\)
\(4x=28\)
\(x=7\)
Vậy x = 7
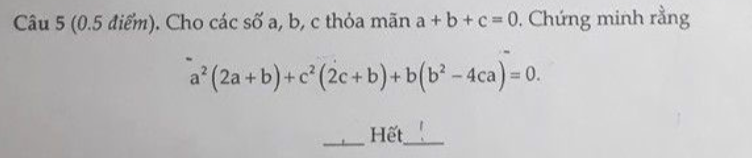

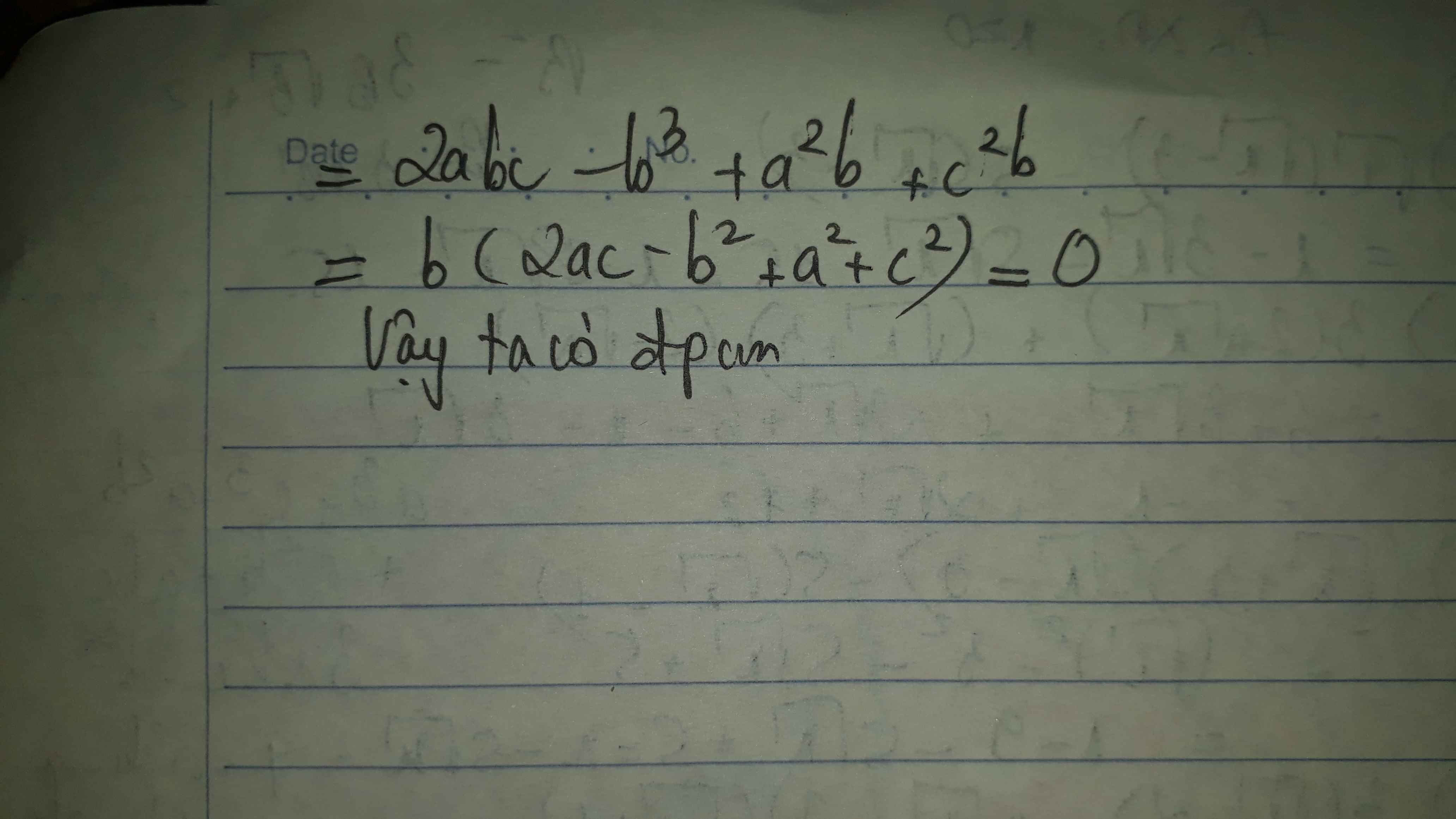

Để A đạt GTLN
=>x2 -2x đạt giá trị dương nhỏ nhất
=>x2-2x=1
=>x2-2x-1=0
=>x=$1-\sqrt{2};\sqrt{2}+1$1−√2;√2+1
Vậy A ko xảy ra GTLN
Để A đạt GTLN
=>x2 -2x đạt giá trị dương nhỏ nhất
=>x2-2x=1
=>x2-2x-1=0
=>x=\(1-\sqrt{2};\sqrt{2}+1\)
Vậy A ko xảy ra GTLN