Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để A đạt GTLN
=>x2 -2x đạt giá trị dương nhỏ nhất
=>x2-2x=1
=>x2-2x-1=0
=>x=$1-\sqrt{2};\sqrt{2}+1$1−√2;√2+1
Vậy A ko xảy ra GTLN
Để A đạt GTLN
=>x2 -2x đạt giá trị dương nhỏ nhất
=>x2-2x=1
=>x2-2x-1=0
=>x=\(1-\sqrt{2};\sqrt{2}+1\)
Vậy A ko xảy ra GTLN

+) (5x-1). (2x+3)-3. (3x-1)=0
10x^2+15x-2x-3 - 9x+3=0
10x^2 +8x=0
2x(5x+4)=0
=> x=0 hoặc x= -4/5
+) x^3 (2x-3)-x^2 (4x^2-6x+2)=0
2x^4 -3x^3 -4x^4 + 6x^3 - 2x^2=0
-2x^4 + 3x^3-2x^2=0
x^2(-2x^2+x-2)=0
-2x^2(x-1)^2=0
=> x=0 hoặc x=1
+) x (x-1)-x^2+2x=5
x^2 -x -x^2+2x=5
x=5
+) 8 (x-2)-2 (3x-4)=25
8x - 16-6x+8=25
2x=33
x=33/2


Làm 1 cách là đủ rồi mà (: 6 cách thì đến bao giờ :v
a) x2 + x - 6 = x2 - 2x + 3x - 6 = x( x - 2 ) + 3( x - 2 ) = ( x - 2 )( x + 3 )
b) x2 - 4x + 3 = x2 - x - 3x + 3 = x( x - 1 ) - 3( x - 1 ) = ( x - 1 )( x - 3 )
c) x2 + 5x + 4 = x2 + x + 4x + 4 = x( x + 1 ) + 4( x + 1 ) = ( x + 1 )( x + 4 )
d) x2 - x - 6 = x2 + 2x - 3x - 6 = x( x + 2 ) - 3( x + 2 ) = ( x + 2 )( x - 3 )
e) 2x2 + 5x + 3 = 2x2 + 2x + 3x + 3 = 2x( x + 1 ) + 3( x + 1 ) = ( x + 1 )( 2x + 3 )
g) 2x2 - 7x + 3 = 2x2 - 6x - x + 3 = 2x( x - 3 ) - ( x - 3 ) = ( x - 3 )( 2x - 1 )
h) 3x2 + 10x - 8 = 3x2 + 12x - 2x - 8 = 3x( x + 4 ) - 2( x + 4 ) = ( x + 4 )( 3x - 2 )
k) \(\frac{1}{2}x^2-\frac{19}{6}x+1=\frac{1}{2}x^2-\frac{1}{6}x-3x+1=\frac{1}{2}x\left(x-\frac{1}{3}\right)-3\left(x-\frac{1}{3}\right)=\left(x-\frac{1}{3}\right)\left(\frac{1}{2}x-3\right)\)

Bài làm :
- Cách 1: x2- 6x + 8
= x2 - 2x - 4x + 8
= x (x - 2) - 4(x -2)
= (x - 4)(x -2)
- Cách 2: x2 - 6x + 8
= x2 - 6x + 9 - 1
= ( x - 3)2 - 1
=( x -3 - 1)( x- 3 + 1)
= (x - 4)(x -2)
- Cách 3: x2 - 6x + 8
= x2 - 16 - 6x + 24
=( x - 4)(x + 4 ) - 6 (x - 4)
=(x - 4)(x + 4 - 6)
= (x - 4)(x -2)
Chúc bạn học tốt !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
mình cũng được tròn 3 cách
c1 \(x^2-6x+8=x^2-2x-4x+8=x\left(x-2\right)-4\left(x-2\right)=\left(x-4\right)\left(x-2\right)\)
c2 \(x^2-6x+8=\left(x^2-6x+9\right)-1=\left(x-3\right)^2-1=\left(x-4\right)\left(x-2\right)\)
c3 Gỉa sử \(x^2-6x+8=\left(x+a\right)\left(x+b\right)=x^2+\left(a+b\right)x+ab\)
Cân bằng hệ số ta được \(\hept{\begin{cases}a+b=-6\\ab=8\end{cases}< =>\orbr{\begin{cases}a=-4\\b=-2\end{cases}or\orbr{\begin{cases}a=-2\\b=-4\end{cases}}}}\)
Vậy ta có : \(\left(x+a\right)\left(x+b\right)=\left(x-2\right)\left(x-4\right)\)

8) \(\left(x+4\right)\left(6x-12\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+4=0\\6x-12=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-4\\6x=12\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=-4\\x=2\end{cases}}}\)
Vậy \(x\in\left\{-4;2\right\}\)
11) \(\left(\frac{7}{8}-2x\right)\left(3x+\frac{1}{3}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}\frac{7}{8}-2x=0\\3x+\frac{1}{3}=0\end{cases}\Leftrightarrow\orbr{\begin{cases}2x=\frac{7}{8}-0\\3x=-\frac{1}{3}\end{cases}}\Leftrightarrow\orbr{\begin{cases}2x=\frac{7}{8}\\x=-\frac{1}{9}\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=\frac{7}{16}\\x=-\frac{1}{9}\end{cases}}}\)
Vậy \(x\in\left\{\frac{7}{16};-\frac{1}{9}\right\}\)
12) \(3x-2x^2=0\)
\(\Leftrightarrow x\left(3-2x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=\frac{3}{2}\end{cases}}\)
Vậy \(x\in\left\{0;\frac{3}{2}\right\}\)
13) \(5x+10x^2=0\)
\(\Leftrightarrow5x\left(1+2x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=-\frac{1}{2}\end{cases}}\)
Vậy \(x\in\left\{0;-\frac{1}{2}\right\}\)
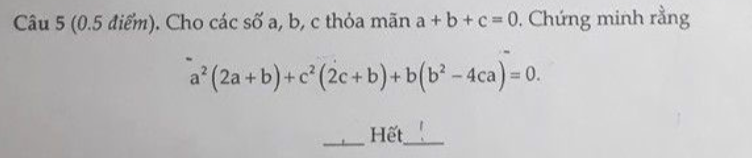

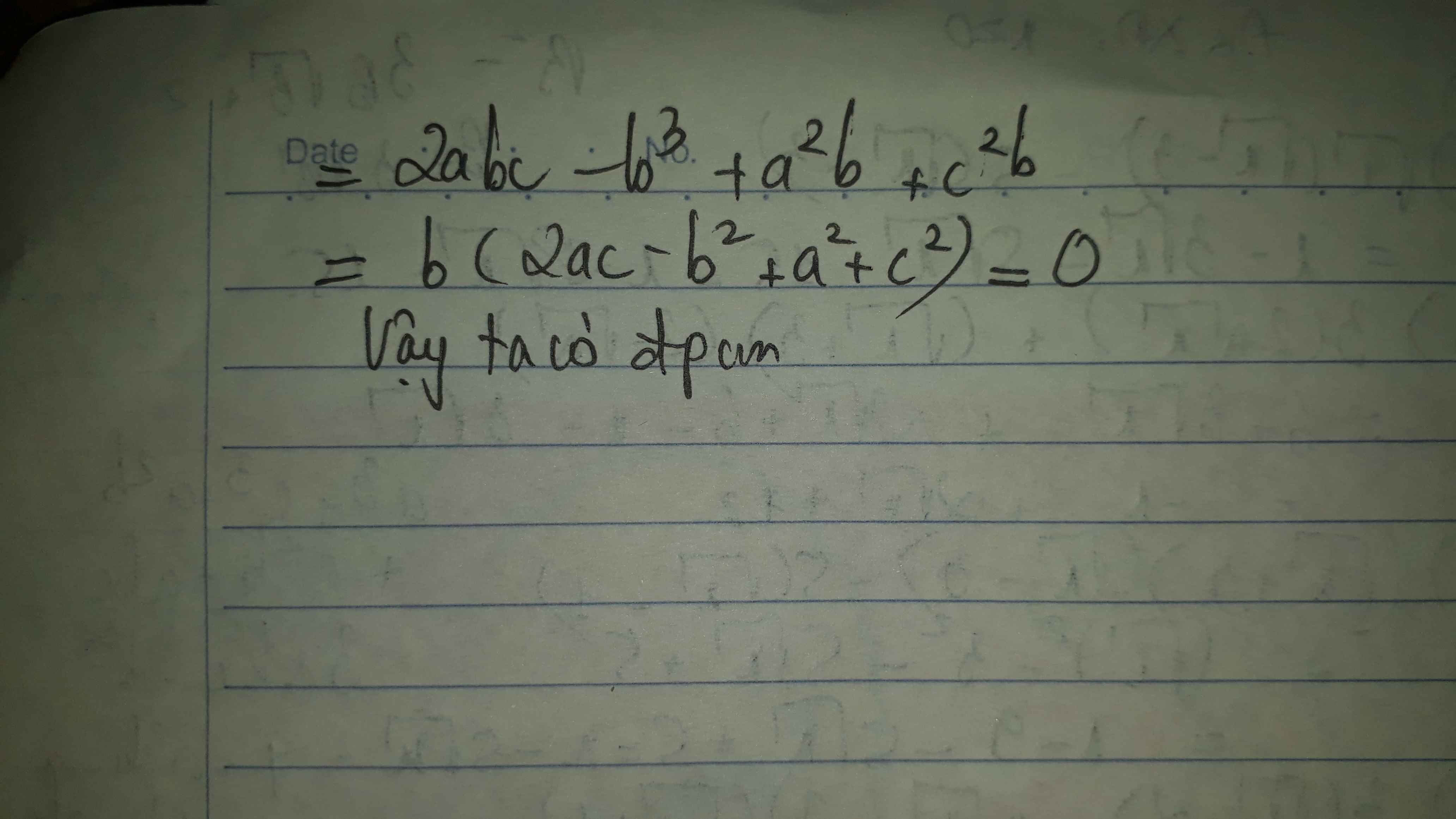
1/ x^2-2x+1-4
(x-1)^2-4
c2: x(x-2)-3