K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
15 tháng 1 2017
Chọn B
Gọi r₁, r₂, r₃, r₄ là khoảng cánh từ điểm M đến bốn mặt của tứ diện.
Gọi S là diện tích một mặt của tứ diện 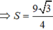
Đường cao của tứ diện là ![]() .
.
Thể tích của tứ diện là 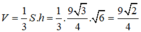 .
.
Mặt khác, ta có:
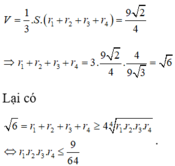

LV
29 tháng 1 2017
PTHĐGĐ của (C) với (d) :
(
ko là nghiệm)
Viết lại: (*).Theo Viet có:
Ta có: nên (C) với (d) luôn cắt nhau tại 2 điểm phân biệt
là giao điểm của (C) với (d)
Theo giả thiết: . Đạt giá trị nhỏ nhất khi
Giải thằng này thu được:

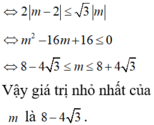
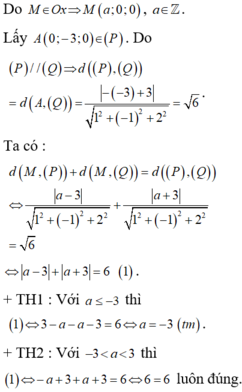


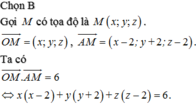
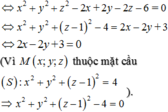
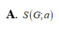
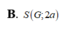

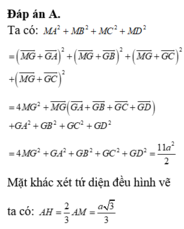

Lời giải:
$M$ nằm trên $Oy$ nên gọi tọa độ điểm $M$ là \((0,a,0)\)
Vì $M$ cách đều $A,B$ nên \(MA=MB\Leftrightarrow MA^2=MB^2\)
\(\Leftrightarrow (1-0)^2+(a-2)^2+(0+1)^2=(0+2)^2+a^2+(0-5)^2\)
\(\Leftrightarrow a^2-4a+6=a^2+29\)
\(\Leftrightarrow 29+4a=6\rightarrow a=\frac{-23}{4}\)
Vậy tọa độ điểm $M$ là \(\left(0,\frac{-23}{4},0\right)\)
cam on nhieu ak